Среднее – это определенная величина (полученная в результате вычислений), которая представляет собой нечто вроде середины в группе данных, обладающих подобными характеристиками и измеряемых в одинаковых единицах. Группой данных могут быть оценки учеников первого класса, рост детей в возрасте 10 лет и т.д. Более точное определение понятия «среднее» приводится в продолжении этой главы.
Как вычисляется среднее?
Мы покажем 3 способа вычисления среднего на примере, относящемся к оценкам 10 учеников четвертого класса за экзамен по математике.
Первый способ: сложение оценок и деление результата на количество учеников
В таблице 3.1 перечислены оценки учеников за экзамен.
Таблица 3.1
|
Ученики (по именам в алфавитном порядке) |
Оценки (в баллах) |
|
Ученик № 1 |
90 баллов |
|
Ученик № 2 |
80 баллов |
|
Ученик № 3 |
70 баллов |
|
Ученик № 4 |
90 баллов |
|
Ученик № 5 |
80 баллов |
|
Ученик № 6 |
70 баллов |
|
Ученик № 7 |
80 баллов |
|
Ученик № 8 |
70 баллов |
|
Ученик № 9 |
70 баллов |
|
Ученик № 10 |
70 баллов |
|
Общая сумма оценок |
770 баллов |
|
Средне |
|
Чтобы вычислить среднее, сначала мы складываем все оценки учеников. В результате получается 770 баллов, и мы делим их на количество учеников и получаем 77 баллов. 77 баллов – это средняя оценка.
Более точное определение среднего
Сумму всех оценок в классе (770 баллов) мы назовем изначальной суммой оценок класса. Среднее – это такая величина, что если бы все 10 оценок в классе были бы одинаковыми и равными среднему, то сумма этих 10 оценок была бы равна изначальной сумме оценок класса.
Другими словами, 77 (среднее) × 10 = 770 баллов.
Второй способ: вычисление вклада каждого ученика в среднее
Как мы вскоре убедимся, каждый ученик прибавляет к среднему какое-то количество баллов. Количество баллов, которое он добавляет, зависит от двух факторов:
-
I. От его оценки — чем больше оценка, тем больше вклад ученика в среднее.
-
От его относительной доли в классе (объяснение следует ниже).
Понятие «относительная доля» означает долю ученика от общего количества учеников в классе.
-
Если в классе 10 ученика, каждый ученик составляет ½, или 10% от класса.
-
Если в классе 2 ученика, каждый ученик составляет ½, или 50% от класса.
-
Если в классе 1 ученик, каждый ученик составляет 1 или 100% от класса.
Чем больше относительная доля ученика, тем больше его вклад в среднее.
Экономисты обычно используют понятие «вес» ученика вместо понятия «относительная доля». В дальнейшем мы тоже будем использовать это понятие (в большинстве случаев).
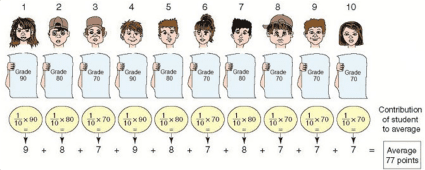
На рисунке 3.1. показан вклад каждого ученика в среднее. Рисунок делится на две части:
-
В части A показаны все десять учеников класса и оценки, которые они получили.
-
В части B показан вклад каждого ученика в среднее и способ его вычисления.
Из рисунка видно, вклад ученика №1 в среднее составляет 9 баллов. Его вклад равен произведению его оценки (90 баллов) и его веса в классе (10%). Вклад ученика №2 составляет 8 баллов (его оценка равна 80 баллов, а его вес равен 10%). Точно так же вычисляется вклад всех остальных учеников вплоть до десятого ученика.
Рисунок 3.1
Третий способ: с помощью групп, состоящих из учеников, получивших одинаковые оценки
Этот способ является наиболее популярным, а во многих случаях и наиболее простым. Чтобы произвести вычисление, мы делим всех учеников класса на группы в зависимости от оценок, которые они получили.
Рисунок 3.2.

Вклад каждой группы в среднее зависит от двух факторов:
-
От оценки группы — чем выше оценка группы, тем выше ее вклад в среднее.
-
От веса группы — вес группы равен общему весу всех учеников в группе.
В нашем примере вес каждого ученика равен 10% (таким образом, вес трех учеников равен 30%, вес пяти учеников равен 50% и т.д.)
На рисунке 3.2. мы видим, что
-
Вклад группы 1 в среднее составляет 18 баллов.
-
Вклад группы 2 в среднее составляет 24 баллов.
-
Вклад группы 3 в среднее составляет 35 баллов.
Итого вклад всех трех групп в среднее составляет 77 баллов. Это и есть среднее.
Систематизация данных в таблице
Таблица 3.2
|
Номер группы |
Значения наблюдений в группе (оценки) |
Количество объектов в группе |
Вес группы |
Вклад группы в среднее |
|
1 |
2 |
3 |
4 |
2 = 5 X 4 |
|
Группа 1 |
90 |
2 |
20% |
18 |
|
Группа 2 |
80 |
3 |
30% |
24 |
|
Группа 3 |
70 |
5 |
50% |
35 |
|
Итого к оплате |
|
10 |
100% |
77 (среднее) |


