Есть случаи, когда слово ожидание заменяет слово среднее. Наиболее распространенный пример это, когда вес (В процентах) в каждой группе получен на основе оценки, вместо того, чтобы сделать точный подсчет числа особей в группе. Тогда мы можем вычислить свою долю целевой группы.
На самом деле, размер целевой группы населения не имеет значения при расчете среднего.
Звучит ли это неясно?
Если так, то путаница может быть вполне ожидаемая. Но мы надеемся, что, когда Вы прочтете примеры, приведенные ниже, Вам все станет ясно уже после второго примера из трех примеров. Примеры очень похожи на те примеры, которые мы уже рассмотрели.
Пример 1: парикмахерская Смита
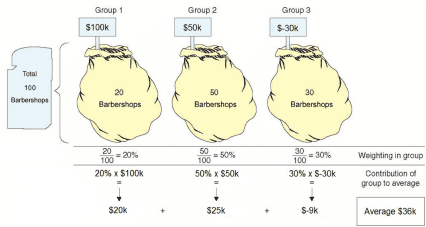
Смиту предложили открыть парикмахерскую. Поскольку Смит – человек очень серьезный и основательный, он решил тщательно исследовать этот вопрос и выяснить, каковы шансы на успех. Для этого он встретил 100 своих друзей, которые сами являются владельцами парикмахерских, и получил от них информацию о рентабельности их парикмахерских. Из информации, которую он получил, вырисовывается следующая картина:
20 парикмахерских приносят прибыль $100k в год.
50 парикмахерских приносят прибыль $50k в год.
30 парикмахерских приносят убыток $30k в год.
Ради удобства мы в очередной раз приводим пример, в котором есть всего 3 значения наблюдений. Из этих данных следует, что большая часть парикмахерских приносит прибыль, и Смита это ободрило. Но он решил действовать более профессионально и вычислил среднюю прибыль на парикмахерскую. В результате у него получилось $36k, согласно расчету, который приводится ниже.
Систематизация данных — упражнение
На этом этапе в каждом примере мы производим систематизацию данных и пользуемся рисунком для их иллюстрации. Но после нескольких примеров Вам уже будет очень легко составлять таблицы данных, и Вы даже сможете сами производить быстрые вычисления.
Исследуемая совокупность: 100 парикмахерских.
Значения наблюдений: $100k, $50k и -$30k.
Деление данных на группы:
Рисунок 3.4
Представление данных в виде таблицы
Таблица 3.8
| Номер группы | Характеристика группы | Значения наблюдений в группе (прибыль за год) | Количество объектов в каждой группе | Вес группы | Вклад группы в среднее |
| 1 | 2 | 3 | 4 | 5 | 3 = 6 X 5 |
| Группа 1 | Нет | $100k | 20 парикмахерских | 20% | $20k |
| Группа 2 | Нет | $50k | 50 парикмахерских | 50% | $25k |
| Группа 3 | Нет | $–30k | 30 парикмахерских | 30% | $-9k |
| Всего | 100 парикмахерских | 100 % | $36k среднее |
Парикмахерская Карлоса
Карлос – новый репатриант из Аргентины. Там он работал парикмахером, и теперь он тоже думает о том, чтобы открыть парикмахерскую. У Карлоса нет друзей среди парикмахеров, но он человек образованный, поэтому он решил обратиться к экономическому консультанту.
Консультант исследовал этот вопрос и представил Карлосу следующее заключение:
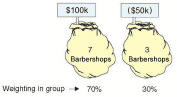
Существует вероятность 70%, что Вы будете получать прибыль $100k в год.
Существует и вероятность 30%, что Вы будете терпеть убыток $50k в год.
Смысл заключения консультанта
Смысл заключения консультанта прост.
По мнению консультанта, если Карлос открыл бы сейчас много парикмахерских (например, 1000), то из них 70% приносило бы ему прибыль $100k в год и около 30% парикмахерских приносило бы ему убыток $50k в год.
Ради удобства мы привели такой пример, в котором заключение консультанта содержит всего два возможных значения наблюдений: прибыль $100k и убыток $50k. Мы не знаем, будет ли заключение консультанта соответствовать действительности или нет, но таково его заключение, и мы предполагаем, что Карлос соглашается с ними.
Вычисление средней прибыли, исходя из заключения консультанта
В этом примере термин «математическое ожидание» используется вместо термина «среднее». Мы производим вычисления двумя способами: Уже известный нам способ.
Мы предполагаем, что Карлос открывает 10 парикмахерских, и что они делятся на прибыльные парикмахерские и убыточные парикмахерские в точном соответствии с прогнозом консультанта.
Краткий способ
Вычисления уже известным нам способом
Систематизация данных:
Исследуемая совокупность — 10 парикмахерских
Значения наблюдений — существует два варианта: $100k и $(50k).
Представление данных в виде рисунка
Представление данных в виде таблицы
Рисунок 3.5
Представление данных в виде таблицы
Таблица 3.9
| Номер группы | Характеристика группы | Значения наблюдений в группе (прибыль парикмахерских) | Количество объектов в каждой группе | Вес группы | Вклад группы в среднее |
| 1 | 2 | 3 | 4 | 5 | 3 = 6 X 5 |
| Группа 1 | Нет | $100k | 7 | 70 % | $70k |
| Группа 2 | Нет | $(50k) | 3 | 30% | $(15k) |
| Итого к оплате | 100 % | $55k математическое ожидание |
Представление данных в виде рисунка
Краткий метод
Предисловие
В своем заключении консультант на самом деле уже разделил наблюдения на группы и дал каждой группе определенный вес. Нам остается всего лишь умножить значения наблюдений на их вес.
Термины с одинаковым значением
- Среднее и математическое ожидание Среднее и математическое ожидание – эти два термина имеют одинаковое значение. В книге «Статистика для начинающих» подробно объясняется, когда правильнее использовать один из терминов, а когда другой. Здесь мы можем только сказать, что правильнее использовать термин «математическое ожидание», когда вычисления основаны на вероятностях, а термин «среднее» – когда вычисления основаны на относительном весе. Относительный вес, вероятности и шансы
- Относительный вес, вероятности и шансы – эти три термина имеют одинаковое значение. В книге «Статистика для начинающих» подробно объясняется, когда правильнее использовать каждый из этих терминов. В этой книге мы не рассматриваем этот вопрос. Каждый может пользоваться ими так, как считает нужным, исходя из конкретной ситуации и из собственной интуиции (которая, как правило, является верной).
Пояснение:
Из слов консультанта мы заключаем, что существует только два возможных варианта значений наблюдений:
- $100k (прибыль)
- $–50k (убыток)
В соответствии с этими значениями формируются две группы. Вес каждой группы – это тот шанс, на который указал консультант, поскольку понятие «шанс» означает, что независимо от того, сколько парикмахерских мы откроем, 70% из них будут находиться в группе $100k, а 30% из них будут находиться в группе $–50k. В соответствии с этим мы заполняем следующую таблицу, не вычисляя данные в графе 5 (она заполняется в соответствии с заключением консультанта):
Таблица 3.10
| Номер группы | Характеристика группы | Значения наблюдений в группе (прибыль парикмахерских) | Количество объектов в каждой группе | Вес группы | Вклад группы в среднее |
| 1 | 2 | 3 | 4 | 5 | 3 = 6 X 5 |
| Группа 1 | Нет | $100k | Не важно | 70 % | $70k |
| Группа 2 | Нет | $-50k | Не важно | 30% | $-15k |
| Итого к оплате | 100 % | $55k математическое ожидание |
Джон тоже думает о том, чтобы открыть парикмахерскую
Неудивительно, что многих людей привлекает перспектива открытия собственной парикмахерской.
К таким людям принадлежит и Джон, который работает в авторемонтной мастерской. У Джона нет друзей среди парикмахеров и нет денег на консультантов, поэтому он попросил помощи у нас. Он просит нас о помощи. Мы предложили ему произвести вычисления общепринятым способом, то есть представить, что он может открыть много парикмахерских, и что годовая прибыль может принимать только 4 значения:
- $100k.
- $70k.
- $20k.
- $-50k.
Мы также предложили ему составить прогноз того, как будут распределяться в процентах его воображаемые парикмахерские между этими четырьмя возможными результатами. Или, другими словами, сколько процентов парикмахерских принесет прибыль $100k, сколько процентов принесет прибыль $70k, сколько процентов принесет прибыль $20k, а сколько процентов парикмахерских принесет убыток $50k.
Мы объяснили ему, что полученные прогнозы он должен поместить в графу 5 таблицы 3.11, и на их основе он должен вычислить данные графы 6 и математическое ожидание. Джон понял наши объяснения и вычислил ожидаемую прибыль.
Таблица 3.11
| Номер группы | Характеристика группы | Значения наблюдений в группе (прибыль парикмахерских) | Количество объектов в каждой группе | Вес группы | Вклад группы в среднее |
| 1 | 2 | 3 | 4 | 5 | 3 = 6 X 5 |
| Группа 1 | Нет | $100k | —— | 20% | $20k |
| Группа 2 | Нет | $70k | —— | 20% | $14k |
| Группа 3 | Нет | $20k | —— | 50% | $10k |
| Группа 4 | Нет | $(50k) | —— | 10 % | $(5k) |
| Итого к оплате | 100 | 100 % | $39k математическое ожидание |
Согласно прогнозам Джона, математическое ожидание прибыли равно $39k.


