Для лучшего обучения, мы используем пример, чтобы представить вам концепцию расчета стандартного отклонения.
В государстве А каждый год проводится чемпионат по броскам в баскетбольную корзину из центра поля.
Каждый баскетбольный клуб посылает на чемпионат одного представителя. Каждый участник чемпионата совершает 10 бросков из центра поля. Победитель чемпионата (игрок, который забросил больше всего мячей) получает приз на сумму $1 млн., тренер его клуба получает примерно ту же сумму.
Тренер баскетбольного клуба » Dream team» хочет выбрать представителя клуба из четырех лучших игроков следующим способом:
-
Для этого он проводит 5 раундов «предварительных бросков». В каждом раунде каждый из игроков должен совершить 10 бросков.
-
Представителем клуба выбирается тот игрок, у которого за 5 раундов в среднем было самое большое количество попаданий.
Результаты раундов приводятся в следующей таблице:
Таблица 3.14
| Игрок 1 | Игрок 2 | Игрок 3 | Игрок 4 | |
| Результаты раунда 1 | 1 попадание | 3 попадание | 6 попадания | 8 попадания |
| Результаты раунда 2 | 0 попадание | 2 попадания | 4 попадания | 2 попадания |
| Результаты раунда 3 | 2 попадание | 4 попадания | 6 попадания | 8 попадания |
| Результаты раунда 4 | Корзина | 0 попадания | 4 попадания | 1 попадания |
| Результаты раунда 5 | 2 попадание | 6 попадания | 5 попадания | 6 попадания |
| Итого попаданий | 5 попадание | 15 попадания | 25 попадания | 25 попадания |
| Среднее количество попаданий на раунд | 1 попадание | 3 попадания | 5 попадания | 5 попадания |
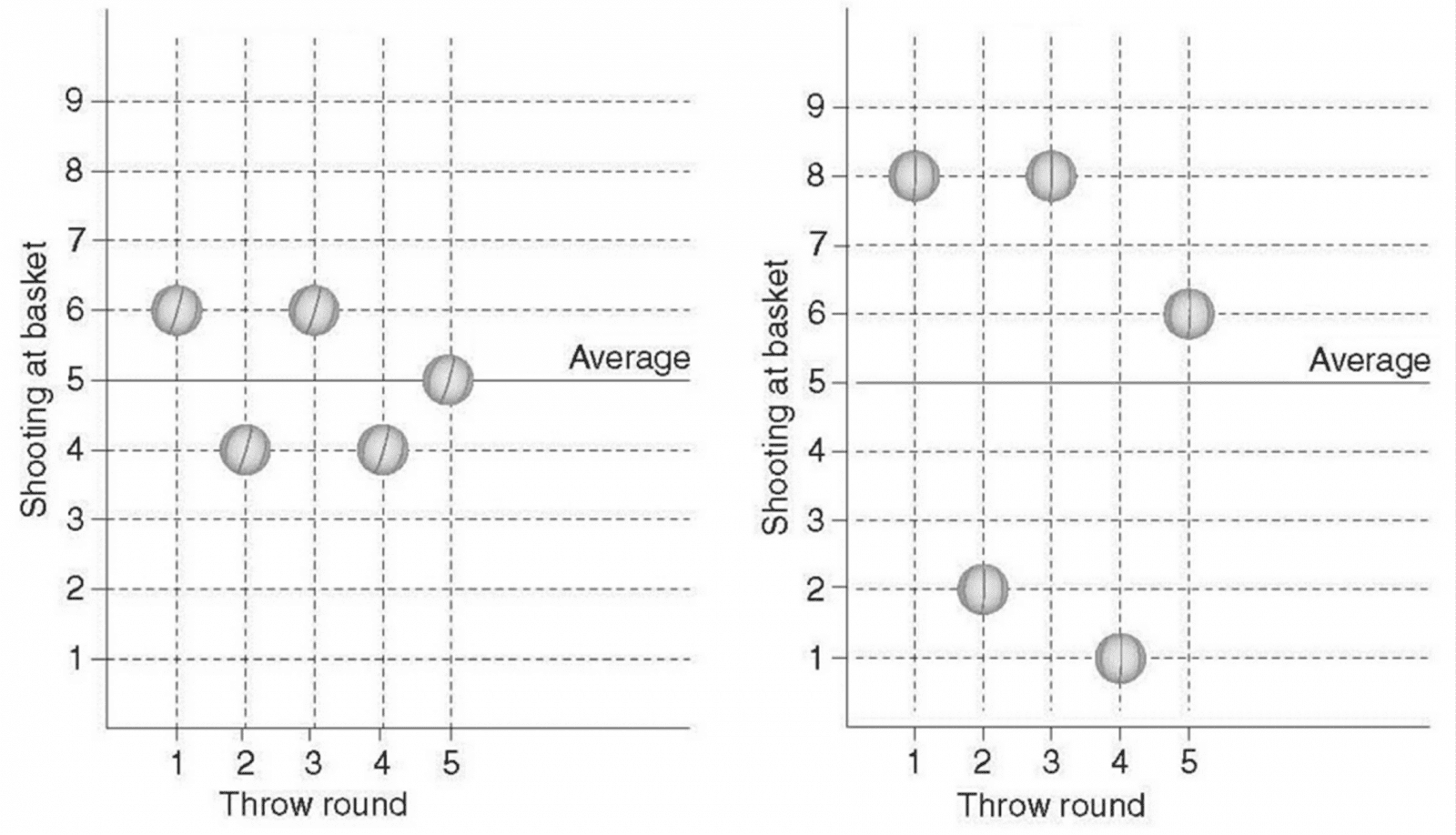
У игроков 3 и 4 в среднем было самое большое количество попаданий на раунд (в среднем 5 попаданий). Тренер клуба » Dream team» должен выбрать одного из них. Он просит Вас помочь ему сделать выбор. Кроме того, он считает нужным подчеркнуть два важных факта:
-
В прошлом году победитель чемпионата в среднем забросил 4 мяча.
-
Если представитель клуба становится победителем, тренер тоже получает $1 млн.
Если Вы посмотрите на таблицу, Вам станет ясно, что следует выбрать игрока №3, поскольку неустойчивость (то есть непоследовательность) его попаданий за пять раундов была относительно невелика, поэтому он подвергает приз тренера меньшему риску, чем остальные игроки.
Если бы игрок №3 продемонстрировал свои теперешние способности на предыдущем чемпионате, у него были бы хорошие шансы на то, чтобы получить первое место, или, как минимум, разделить победу с другим игроком, поскольку он ни в одном раунде не забросил менее четырех мячей. С другой стороны, у игрока №4 наблюдалась более высокая неустойчивость попаданий за пять раундов. Если бы он участвовал в прошлогоднем чемпионате, существовала бы вероятность того, что он забросит менее четырех мячей за раунд.
Неустойчивость (попаданий) рассматривается как фактор риска
Для дальнейших объяснений мы будем пользоваться словом «нестабильность» вместо слова «неустойчивость». Слова «нестабильность» и «неустойчивость» могут заменять друг друга в трех ситуациях:
-
Нестабильность = Неустойчивость
-
Абсолютная стабильность = Отсутствие неустойчивости
-
Высокая стабильность = Низкая неустойчивость
По мнению большинства людей, неустойчивость попаданий игрока №4 подвергает приз тренера большему риску, чем неустойчивость попаданий игрока №3, несмотря на то, что у обоих игроков в среднем наблюдалось одинаковое количество попаданий. В области финансов неустойчивость всегда ассоциируется с риском. Чем выше неустойчивость, тем большим считается риск.
Пример:
Смит купил акции двух банков: банка А и банка В. За акции каждого банка он заплатил $1000, итого $2000. В конце каждого месяца банки извещали Смита о прибыли от его инвестиции за этот месяц, и он записывал эти данные в таблицу 3.15.
Проценты прибыли за каждый месяц начисляются на изначальную сумму инвестиции.
Например, за первый месяц он получил прибыль $10 (1% от $1000) от банка А и прибыль $30 (3% от $1000) от банка В. Смит записал в таблицу 3.15 свою прибыль в процентах.
За второй месяц он снова получил от банка А прибыль $10 (1%), а от банка В он получил убыток $20 (-2%). За шестой месяц он опять получил от банка А прибыль $10 (1%), а от банка В он получил убыток $50 (-5%).
Таблица 3.15. Месячная прибыль (в %) от акций каждого банка Проценты прибыли начисляются на начальную сумму инвестиции ($1000, вложенные в акции каждого банка).
| Месяц | Акции банка A | Акции банка B |
| 1ый месяц | 1% | 3% |
| 2ой месяц | 1 | -2% |
| 3ий месяц | 1 | 5% |
| 4ый месяц | 1 | -3 |
| 5ый месяц | 1 | 8% |
| 6ой месяц | 1 | 5% |
| Средняя прибыль за месяц | 1 | 1 |
Через 6 месяцев Смит вычислил свою среднюю прибыль от каждого банка.
К своему удивлению он обнаружил, что каждый банк в среднем приносил ему прибыль 1% в месяц (или $10 в месяц). Средняя прибыль от обоих банков совершенно одинакова. Но если мы посмотрим на неустойчивость месячной прибыли, мы увидим, что прибыль от банка А была абсолютно стабильной, в то время как в банке Б наблюдалась сильная неустойчивость. Прибыль от этого банка является нестабильной, поэтому на нее трудно рассчитывать.
Когда оба банка в среднем приносят одинаковую месячную прибыль, мы предпочитаем вкладывать в акции, которые отличаются меньшей неустойчивостью. Другими словами, мы предпочитаем более стабильную месячную прибыль.
Измерение неустойчивости
Вернемся к примеру чемпионата по баскетболу. Когда мы предпочли игрока №3 игроку №4, мы исходили только из зрительного впечатления. Но экономисты изобрели более «научный» инструмент для анализа неустойчивости. Этот инструмент удивительно прост. Он называется «стандартное отклонение» и обозначается греческой буквой σ.
Вычисление стандартного отклонения игрока №4
Вычисления показываются с помощью таблицы 3.16.
-
Колонка 2 — количество попаданий, сделанных в каждом раунде. Средняя (5 попаданий) в строке 6. Среднее обычно обозначается буквой М.
-
Графа 3 — подстановка среднего в каждую строку графы 3.
-
Графа 4 — вычисление разности между количеством попаданий в каждом раунде (графа 2) и среднем количеством попаданий (графа 3).
-
Графа 5 — в каждой строке записывается значение разности из графы 4, возведенное в квадрат (например, в строке 4: -42= 16). В строке 6 вычисляется среднее всех цифр, записанных в этой графе (= 8,8).
-
Графа 6 — в строке 6 вычисляется квадратный корень из среднего, вычисленного в графе 5 (= 8,8). Полученный результат является стандартным отклонением (= 2,966).
Использование слова «расстояние» вместо слова «разность»
Во многих случаях правильнее говорить: «расстояние от среднего», а не «разница со средним».
Например, когда мы измеряем рост детей, лучше сказать: «Расстояние между результатом и средней составляет 20 см», чем: «Расстояние между результатом и средней составляет 20 см».
Таблица 3.16
| Номер раунда | Количество попаданий за раунд | Среднее количество попаданий (М) | Разница между количеством попаданий за раунд и средним | Разница в квадрате | Квадратный корень |
| Раунд 1 | 8 | 5 | 3 | 9 | |
| Раунд 2 | 2 | 5 | -3 | 9 | |
| Раунд 3 | 8 | 5 | 3 | 9 | |
| Раунд 4 | 1 | 5 | -4 | 16 | |
| Раунд 5 | 6 | 5 | 1 | 1 | |
| 5 среднее | 8,8 среднее | √8,8=2,966 стандартное отклонение |
Единицы измерения стандартного отклонения
Стандартное отклонение измеряется в тех же единицах, в которых измеряются сами значения наблюдений.
-
Когда наблюдения – это рост детей в сантиметрах, стандартное отклонения измеряется в сантиметрах.
-
Когда наблюдения – это количество попаданий в корзину, стандартное отклонения измеряется в попаданиях.
-
Когда наблюдения – это вес продуктов в килограммах, стандартное отклонения измеряется в килограммах.


