We will usually not obtain a smooth bell-shaped normal curve in the samples that we take. In most cases, the curve will only be similar to a bell curve but not identical.

The probability distribution that we receive is called the sample probability distribution.

For example, if we measure the weight of the fish in Lake Michigan, we may get a probability distribution like the one in this example.

Calculating the Probabilities of a Sample Probability Distribution That is in the Form of a Normal Curve

Statisticians have not yet found a way to calculate probabilities from a normal probability distribution based on a sample that is not an exact normal curve, i.e., a smooth and symmetrical bell-shaped curve. In these cases, the solution is to use a normal curve that is closest to the sample probability distribution. We will use this normal curve to make probability calculations.

The probabilities we obtain on the basis of the normal curve will obviously be only an approximation (and sometimes a crude one) of the probabilities we should have obtained for the sample probability distribution, were there a way of calculating them.

The more professional and experienced a statistician is, then the better he or she will be able to make use of the significance of the approximate results, and to estimate the level of error that may exist.

The more general and approximate the picture that we want to derive from the data, then the less important it is to be precise, and the more likely is it for the approximated data to satisfy our purposes.

Calculating the Probabilities of Any Normal Curve

Understanding the Probability of Normal Distribution Curve

Example:

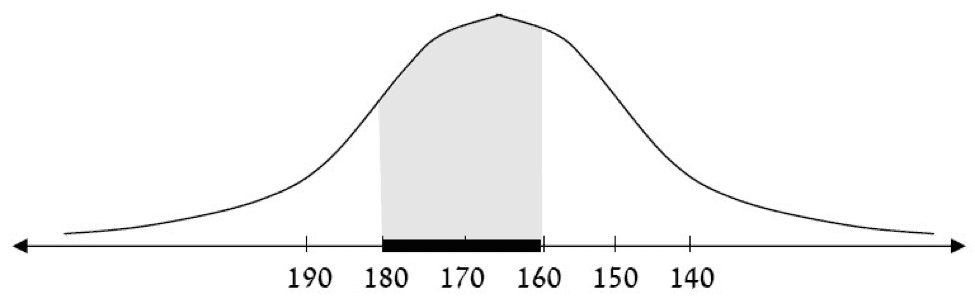
We ask ourselves the following question: If we randomly choose one person from a crowd of people celebrating Independence Day, then what is the probability that this individual’s height will be between 150 centimeters and 170 centimeters?

We assume that, according to a sample that we have conducted, the crowd of celebrating people has the normal distribution curve (the normal curve of the sample), which is extremely close to the normal curve (the exact curve) as presented in the above diagram, in which ?= 167 centimeters and ? = 2 centimeters. Actually, we are interested in calculating the probability that some specific event will occur.

Every Person Whose Height is Between 150 Cm and 170 Cm

We will mark this event on the number axis with a black stripe beginning at 150 centimeters and ending at 170 centimeters.

The probability that this event will occur is represented by the area under the curve and above the stripe.

The relevant area for the event is always less than 100%, since the entire area under the bell-shaped curve is equal to 100%.

Diagram