We will again consider the two events with an overlap between them:

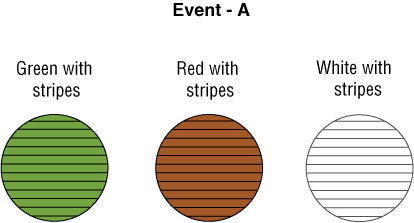
Event A – drawing out balls with stripes.

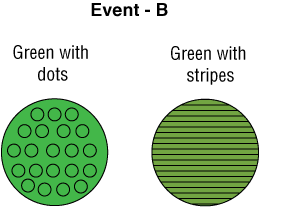
Event B – drawing out a green ball.

What is the probability that at least one of these two events will occur?

(You will find out the answer on the next slide.)

We can combine these two events into a single event:

The size of the united event is 4.

The size of the sample space is 5 (since there are five balls in the container). The probability that we are seeking is therefore 4/5.

The Calculation When the Events are Mutually Exclusive

We will consider the two mutually exclusive events:

Event A – drawing out a ball with stripes.

Event B – drawing out a green ball with dots.

Green with dots

Here, too, we can combine the events into a single event:

We reach the conclusion that the probability that at either Event A or Event B will occur is ⁴/₅.

(Explanation: 4 balls (out of 5) can cause the combined event to occur).

Here, however, because the events are mutually exclusive, we can use a different method:

Stage 1: We calculate the probability of Event A, and obtain ³/₅, i.e., 3 balls (out of 5) can cause Event A to occur.

Stage 2: We calculate the probability of Event B, and obtain ¹/₅ , i.e., 1 ball (out of 5) can cause Event B to occur.

Stage 3: We add these two probabilities (Stage 1 and Stage 2), and obtain ⁴/₅.

Complementary Events – Example and Explanation

We will again consider the two events.

• Event A – drawing out a ball with stripes.

• Event B – drawing out a green ball with dots.

In this case, we can also calculate the probability that one of these combinations will occur as a complementary event.

There is only one ball (i.e., red with dots) that can be removed without causing Event A or Event B to occur. Drawing out a red ball with dots therefore represents a complementary event relative to the combination of Events A and B. The probability of drawing out a specific ball is 1/5. Drawing out any other ball must cause either Event A or Event B to occur.

The probability that either Event A or Event B will occur is therefore 1 – 1/5 = 4/5.