There are various types of bell-shaped curves.
They look similar, but each bell-shaped curve has two characteristics that differentiate it from the other bell-shaped curves. These characteristics are as follows:
-
The location of μ on the number axis.
-
The degree of convexity of the curve (i.e., whether it is narrow and high, or wide and low).
Example 1: Two bell-shaped curves with the same convexity, but different locations relative to μ .
Diagram

Example 2: Two bell-shaped curves with the same locations relative to μ, but different degrees of convexity.
Diagram
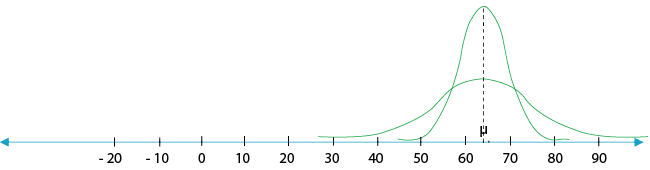
Example 3: Two bell-shaped curves with the same locations relative to μ, but different degrees of convexity.
Diagram

The degree of convexity of a bell-shaped curve reflects the degree of dispersal of its probability distribution. The narrower and higher the bell-shaped curve, then the closer most of the results will be to the expectation, which means less dispersal. The wider and lower the bell-shaped curve, then the more widely dispersed the results will be The statistical measure of the degree of dispersal reflects the standard deviation. Probability distributions with a low standard deviation reflect narrower and higher bell-shaped curves, while probability distributions with a high standard deviation reflect wider and lower bell-shaped curves.


