Question: What is the probability of obtaining values between 0 and 0.5 (i.e., the area shaded in gray)?
Diagram
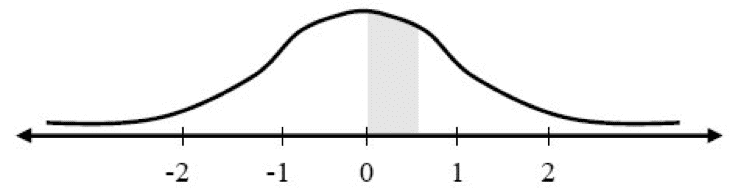
Answer: 0.1915
Explanation: In order to find the area shaded in gray, the following subtractions should be performed:
|
The area under the curve to the left of 0.5 |
= 0.6915 |
|
The area under the curve to the left of 0 |
= 0.5000 |
|
The result |
0.1915 |
Question: What is the probability of obtaining values between –1.5 and 1.5?
Diagram
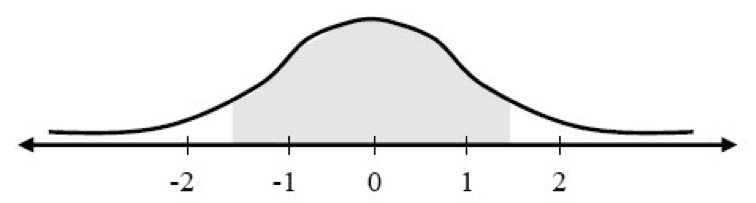
Answer: 0.8664
Explanation: The area under the curve to the left of 1.5 is 0.9332, and the area under the curve to the left of -1.5 is 0.0688. Subtracting the second number from the first will provide the area shaded in the diagram, which is the desired probability: 0.9332 – 0.0668 = 0.8664.
Question: What is the probability of obtaining values greater than 1.5 or less than –1.5?
Diagram
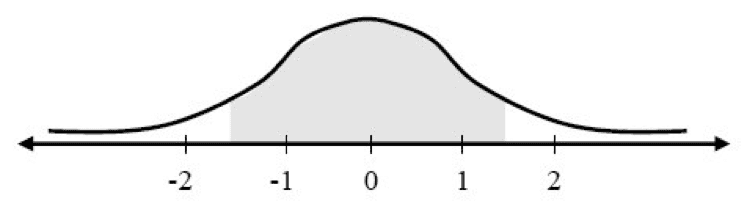
Answer: 0.1336
Explanation – Method A: The easiest way is to consider that the area in this question is exactly complementary to the area in the preceding question. This means that the sum of the areas in this question and the preceding question is 1. If we subtract the area obtained in the preceding question from 1, we will therefore obtain the answer to this question: 0.1336 = 1 – 0.8664.
Method B: We will find the area to the left of –1.5, which is 0.0668, in the table. Since the bell-shaped curve is symmetrical, the area to the right of 1.5 is identical, i.e., 0.0668. The total shaded area is therefore 2 x 0.0668 = 0.1336.


