Probability of an event:
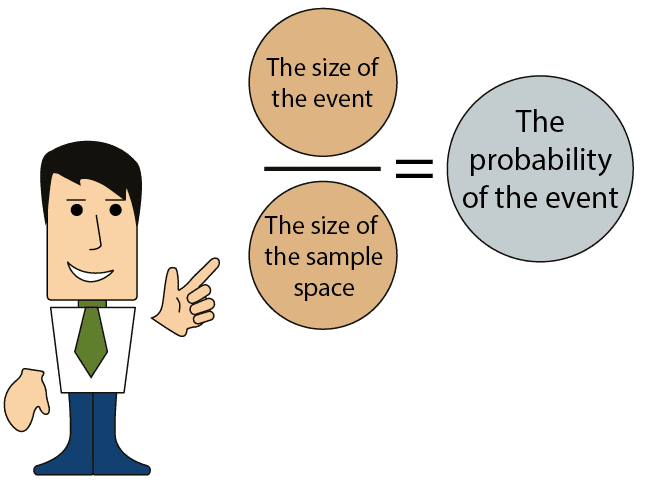
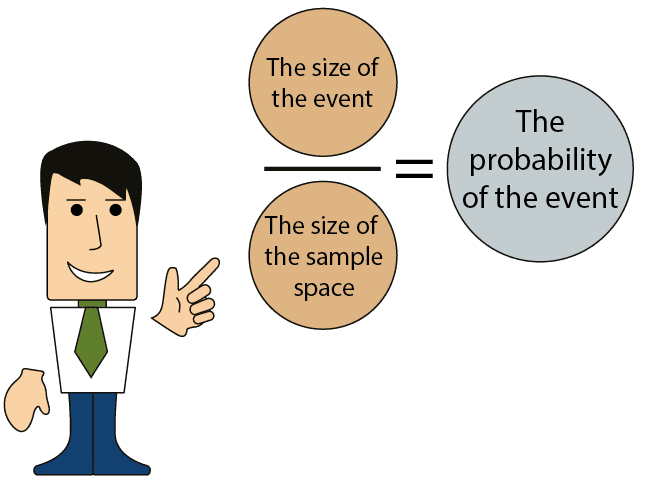
In order to calculate the probability of an event occurring, we will need the following data:
-
The size of the event.
- The size of the sample space.
Dividing the first number by the second number provides the probability of the event occurring.
Example 1 – the probability of obtaining an odd number when throwing one of the dice
The trial: Throwing one of the dice.
The event (in words): An odd number is obtained.
From the defined terms of the trial, we can identify the sample space and its size:
The sample space: 1, 2, 3, 4, 5, and 6.
Size of the sample space: 6.
The sample space: 1, 2, 3, 4, 5, and 6.
Size of the sample space: 6.
From the defined terms of the event, we can describe it numerically and find its size:
The event: 1, 3, and 5.
Size of the event: 3.
In order to calculate the probability of the event, we will need to know the size of the event (3) and the size of the sample space (6).
If we divide the first number by the second, then we will obtain the probability of an odd number event: i.e., 3/6 = 1/2.
|
1 – 1 |
1 – 2 |
1 – 3 |
1 – 4 |
1 – 5 |
1 – 6 |
|
2 – 1 |
2 – 2 |
2 – 3 |
2 – 4 |
2 – 5 |
2 – 6 |
|
3 – 1 |
3 – 2 |
3 – 3 |
3 – 4 |
3 – 5 |
3 – 6 |
|
4 – 1 |
4 – 2 |
4 – 3 |
4 – 4 |
4 – 5 |
4 – 6 |
|
5 – 1 |
5 – 2 |
5 – 3 |
5 – 4 |
5 – 5 |
5 – 6 |
|
6 – 1 |
6 – 2 |
6 – 3 |
6 – 4 |
6 – 5 |
6 – 6 |

Example 2 – the probability of obtaining the same number twice when throwing two dice
The trial: Throwing two dice simultaneously.
The event (in words): Two of the same numbers are obtained. From the definition of the event, we can identify the sample space and its size:
Sample Space: When throwing a pair of dice, it is possible to obtain all of the pairs as in the following list:
Key: Regular – a white die.
The first row includes all of the possible pairs with the number 1 on the white die.
The second row includes all of the possible pairs with the number 2 on the white die, and so on and so forth
Size of the sample space: 36 (i.e., there are 36 possible pairs in the diagram).
From the defined terms of the event, we can describe it in numerically, and identify its size:
The event: (1,1), (2,2), (3,3), (4,4), (5,5), (6,6).
Size of the event: 6.
In order to calculate the probability of an event, we need to know the size of the event (6) and the size of the sample space (36). If we divide the first number by the second, we obtain the probability of an event when the throwing of two dice results in two identical numbers: i.e., 6/36 = 1/6 .