In situations of uncertainty, investment decisions are based on evaluations of the probability of success on the one hand, or of failure and loss on the other.
When losing money on a given investment is a possibility, the character of the person making the decision also affects his or her decisions – to what degree he or she is mentally and financially willing to take risks upon themselves. We will illustrate the point through examples.
Character Traits: “Risk Averse” Versus “Risk Seeking”
A person has $100 and plans to buy a lottery ticket with this money. The prize is $200, and the probability of winning is 50%, meaning that half of the people who buy a ticket win $200, and half do not (they lose their money).
A “risk averse” person will not buy the ticket because he prefers keeping $100 in his pocket as opposed to the risk of losing it (the temptation of winding up with $200 in his pocket does not affect his or her decision). If a person is “risk seeking”, the temptation of a possible profit will cause him to buy the lottery ticket (the chance that he will potentially lose $100 does not deter him).
What would you, the reader, choose? The answer depends on your attitude toward risk. Are you risk averse or risk seeking?
Assume that you are risk averse, i.e., you would not have bought the lottery ticket under the current circumstances. Now, let us try to examine what you would do under two scenarios, if the conditions are adjusted in your favor.
Scenario 1:
The prize is increased from $200 to $200,000 (the probability of winning remains 50%). Will the fear of losing still be stronger than the temptation of winning the prize?
Scenario 2:
The prize is still $200, but the probability of winning rises to 99%, i.e. it is almost certain that you will win. Will you still choose not to buy the ticket? If these changes in the lottery terms still did not change your decision not to buy the ticket, then you are extremely risk averse.
We now assume that you are risk seeking, i.e. you buy the lottery ticket under the original terms. We will examine your behavior under two scenarios in which the conditions change to your detriment.
Scenario 1:
The prize drops from $200 to $101. Will you still buy the ticket?
Scenario 2:
The prize remains $200, but the probability of winning it drops to 1% (you will almost surely lose). Will you then buy the ticket? If so, then you very much like taking a risk, and it may be that the taking of the risk itself benefits you beyond the financial benefit of the prize.
We have therefore seen that the decision whether or not to take a risk is not an objective decision. It changes from one person to another depending on their character. In order for a person to make a decision that suits his or her character, they must be capable of objectively analyzing the probability of success and the associated amount of money, as compared with the probability of failure and consequent monetary loss.
For example, if the chance of winning $100 is 60% and the chance of losing $100 is 40%, then it is objectively worthwhile taking part in the lottery.
For example, if the chance of winning $1,000 is 20% and the chance of losing $1,000 is 80%, then it is not worthwhile taking part.
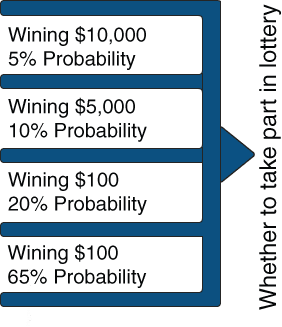
In these examples, we assumed that there are only two possibilities: Winning and losing – each with its own probability. In most cases, however, there are more than two possibilities, as in the following example (four possibilities):
- Winning $10,000 – 5% probability.
- Winning $5,000 – 10% probability.
- Winning $100 – 20% probability.
- Losing $100 – 65% probability.
In order to decide whether to take part in a lottery with these four possible outcomes, it is customary to calculate the expected profit, but that will be explained later.