如何计算标准差

举例说明

A国每年举行一次半场投篮手比赛。

每个篮球队派一名代表参赛。每个选手从中场开始投10次篮。获胜者（投篮命中率最高的人）可获得$1,000,000的奖金，而且他的教练也可获得同样的奖金。

在梦之队篮球队，教练要从四名优秀球员中挑选一人参赛，方法如下:

• 他让每个球员投篮五轮，每轮投10个半场球。

• 他会选择五轮中具有最高平均数的球员。

下表说明了球员的各轮投篮结果:

表 3.14

	球员 1	球员 2	球员 3	球员 4
第1轮结果	1 球	3 球	6 球	8 球
第2轮结果	0 球	2 球	4 球	2 球
第3轮结果	2 球	4 球	6 球	8 球
第4轮结果	0 球	0 球	4 球	1 球
第5轮结果	2 球	6 球	5 球	6 球
总进球数	5 球	15 球	25 球	25 球
每轮平均	1 球	3 球	5 球	5 球

 

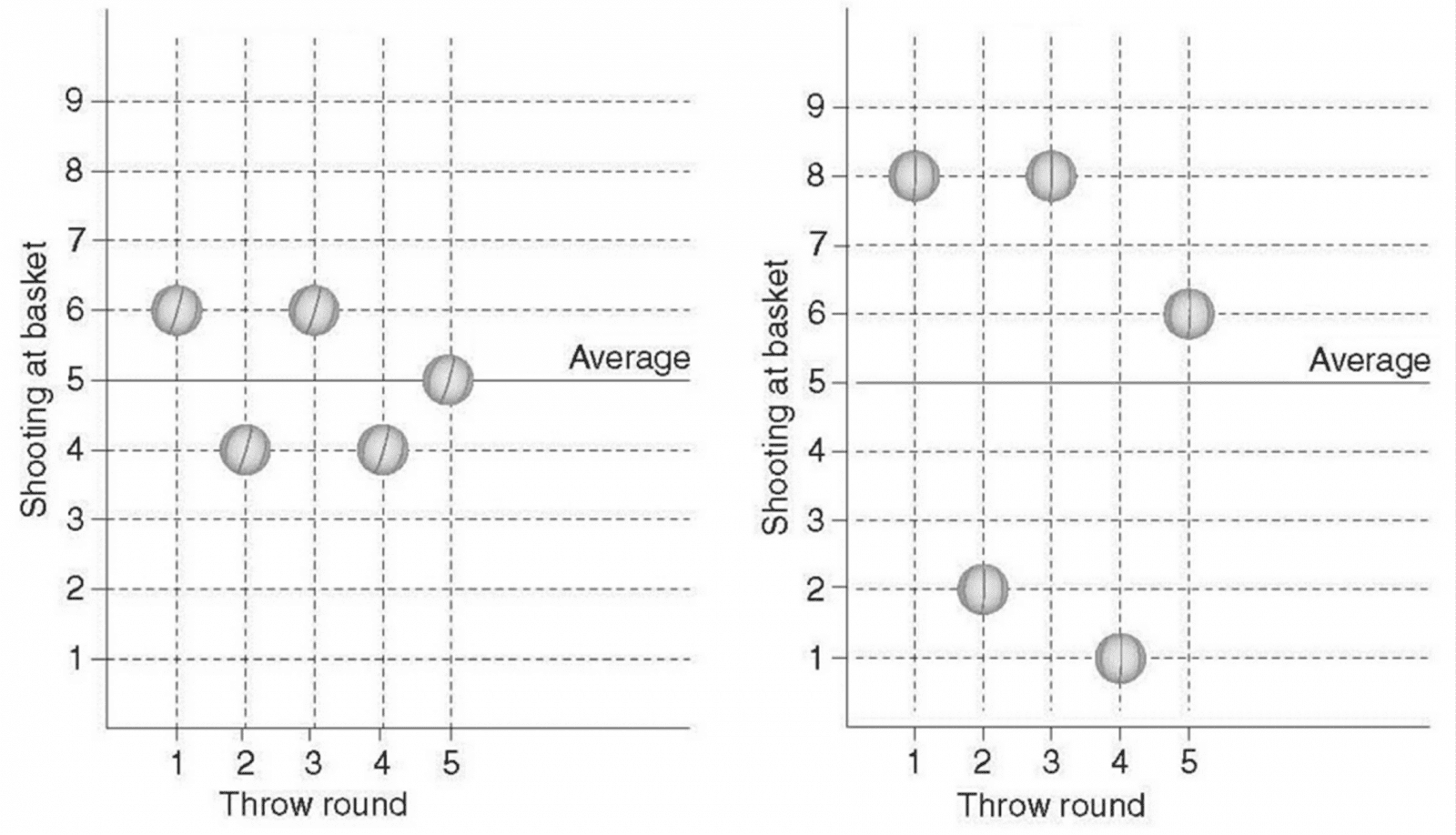
球员3和 球员4每轮的进球数最多 (平均每轮5球)。梦之队的教练必须在他们之间做出选择，他向你寻求帮助。他同时还提供两个重要信息:

1. 去年比赛的获胜者每轮的平均进球数是4。

2. 如果自己的球员获胜，教练将获得$1,000,000的奖金。

从结果上看，你很可能会选择球员3，因为他每轮投篮的波动性 (即缺乏稳定性)更小，从而为教练赢取奖金的几率就更大。

如果球员3在去年参加比赛并表现他的实力，他获得或至少分享第一名的可能性极高，因为他每轮的进球数都不低于4个。另一方面,球员4各轮之间的波动性比较大。如果他已经参加去年的比赛,他也有可能取得了低于4球的成绩。

（得分）波动性被视作风险因素

在下面的说明中，我们将使用不稳定性来代替波动性。下列描述解释了不稳定性和波动性之间的三种关系:

1. 不稳定性 = 波动性。

2. 完全稳定性 = 没有波动性。

3. 较大的稳定性 = 较少的波动性。

大多数人认为球员4的波动性相对于球员3的稳定发挥来说，会更容易影响到教练获得奖金的几率，虽然他们的平均进球数相等。在金融领域，风险与波动性有关。波动性越大，风险越大。

示例：

史密斯买进了两家银行的股票：A银行和B银行。A银行和B银行，他从每个银行购买$1,000的股份,总额为2,000美元。在每个月的月底,投资的利润每月都会进行报告,并且他会将结果记录在表中。

每月利润的百分数与原始投资额有关。

例如,在第一个月,他从A银行获得了10美元($1000的1%),B银行获得30美元($1000的3%)。他将盈利以百分比的形式记录在表中。

在第二个月,他再次从A银行获得10美元(1%),在B银行失去了20美元(2%)。到了第六个月,他再次从A银行获得10美元(1%),在B银行失去了50美元(5%)。

表 3.15 – 每家银行股票的月利润数据（用百分数表示）

月份	A银行股票	B银行股票
1月	1%	3%
2月	1%	-2%
3月	1%	5%
4月	1%	-3%
5月	1%	8%
6月	1%	-5%
月平均利润	1%	1%

 

在第6个月底，史密斯计算每家银行的平均利润。

他惊讶的发现，平均而言，他在每家银行上每月赚取1% (or $10)的利润 – 数值完全相同。但是，当我们研究每月的波动性时，发现A银行的股票利润非常稳定，而B银行的股票利润则极不稳定。如果利润不稳定的话，就靠不住。

在此情形中，当两种股票都创造同样的平均月利润时，我们宁愿选择投资波动性较低的股票，换言之，月利润更稳定的股票。

波动性的衡量

再回到投篮的例子。选择3号球员而不是4号的决定完全取决于初浅的印象。但是，经济学者发明了一种简单且又能“评估波动性的科学工具”。这个工具称为标准差，用希腊字母σ表示。

计算球员4的标准差

用表 3.16计算。

1. 第2栏 – 每轮的进球数。平均值(5篮)插入行6。字母M是通常用于表示平均值。

2. 第3栏 – 平均数。

3. 第4栏每轮进球数（第2栏）与平均进球数（第3栏）之差。

4. 第5栏是第4栏的差数的平方（例如，在第4栏中(-4)² =16)。第6行是该栏前五行的平均数 (8.8)。

5. 第6栏是第5栏平均数的平方根。分两步计算：第5栏的平均值(8.8)，并求其平方根 (2.966)。

使用“差距”来代替“差异”

在多数情况下，用“与平均数的差距”来代替“与平均数的差异”会更合适。

例如,当测量儿童的高度,更恰当的说法是:”结果和平均数之间的差距为20cm”而不是:”结果和平均数之间的差距为20cm”而不是:

表 3.16

轮数	该轮的进球数	平均进球数 (M)	进球数与平均数的差距	差的平方	平方根
第1轮	8	5	3	9
第2轮	2	5	-3	9
第3轮	8	5	3	9
第4轮	1	5	-4	16
第5轮	6	5	1	1
	5（平均）			8.8（平均）	√8.8=2.966 标准差

标准差的衡量单位

标准差的测量单位与结果数据的单位相同。

1. 当数据是孩子的身高（用厘米表示）时，标准差以厘米衡量。

2. 当数据是进球数时，标准差以进球数衡量。

3. 当数据是鱼的重量时（用千克表示），标准差以千克衡量。