La expectativa no es una medida suficiente para describir una distribución.
Es posible que existan dos distribuciones con exactamente la misma expectativa teniendo naturalezas completamente diferentes. Ahora ilustraremos esto por medio de un ejemplo. Consideraremos las siguientes dos distribuciones:
- Distribución A
El valor La Probabilidad 2 0,3 3 0,25 5 0,25 7 0,2 Total 1 - Distribución B
El valor La Probabilidad 0 0,25 1 0,25 7 0,25 8 0,25 Total 1
Si, sin embargo, insistimos en ejemplos realistas, podemos imaginar dos ruecas:
- Una rueda que gira tiene los números 2, 3, 5 y 7 que aparece en él. Una vez más, esta rueda de hilado no está equilibrada, lo que significa que ciertos números son más probable que aparezca que otros. Esta rueda de giro corresponde a Distribución A.
- La segunda rueda giratoria tiene los números 0, 1, 7 y 8 que aparece en él. Además, esta rueda de giro no se equilibra de tal manera que ciertos números son más propensos a aparecer de otros.Este rueda de giro corresponde a la distribución B.
Calcularemos la expectativa de estas dos Distribuciones:
Distribución A: (0.3 x 2) + (0.25 x 3) + (0.25 x 5) + (0.2 x 7) = 4
Distribución B: (0.25 x 0) + (0.25 x 1) + (0.25 x 7) + (0.25 x 8) = 4
La expectativa de las distribuciones es idéntica: 4 Pero, ¿son estas distribuciones idénticas?
Veremos un diagrama de líneas de las distribuciones (la línea punteada denota la expectativa):
Distribución A
Diagrama
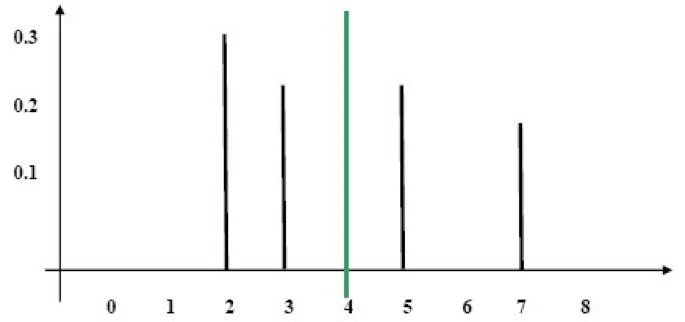
Distribución B
Diagrama
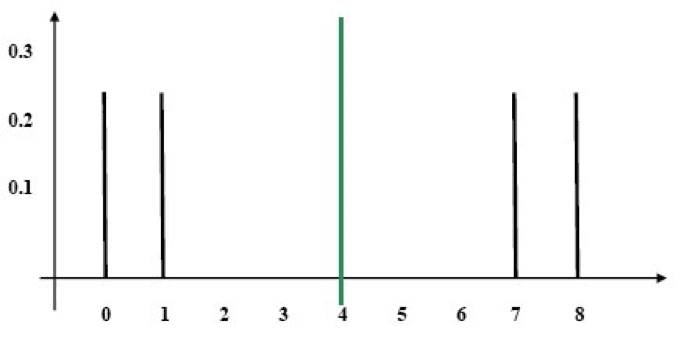
Es fácil ver que la Distribución B está más dispersa alrededor de la expectativa que la Distribución A. Por lo tanto, usaremos una medida de dispersión. Una medida de dispersión es un número que en efecto, expresa la expectativa de la desviación de la expectativa.
Sin embargo, por razones matemáticas, nuestro cálculo es un poco más complejo e incluye elevar al cuadrado y obtener la raíz cuadrada. La medida de dispersión es la desviación estándar. El método para calcular la desviación estándar en el caso de una probabilidad es idéntico al método para calcular la desviación estándar de una muestra.
Agregaremos una tercera columna la cual llenaremos con la expectativa, y una cuarta columna en la cual escribiremos la desviación de la expectativa (el resultado de substraer la expectativa del valor).
La quinta columna es el cuadrado de la desviación:
| El valor | La Probabilidad | la Expectativa | La Desviación de la Expectativa | La Desviación al Cuadrado |
| 2 | 0,3 | 4 | 2 – 4 = -2 | (-2)2 = 4 |
| 3 | 0,25 | 4 | 3 – 4 = -1 | (-1)2 = 1 |
| 5 | 0,25 | 4 | 5 – 4 = 1 | 12 = 1 |
| 7 | 0,2 | 4 | 7 – 4 = 3 | 32 = 9 |
| Total | 1 |
Ahora calcularemos la expectativa del cuadrado de la desviación.
Multiplicamos la columna 2 por la columna 5 y sumamos: (0.3 x 4) + (0.25 x 1) + (0.25 x 1) + (0.2 x 9) = 3,5
La desviación estándar es la raíz cuadrada del resultado que hemos obtenido (3.5): 3,5/1,87
De la misma manera, calcularemos la desviación estándar para la Distribución B:
| El valor | La Probabilidad | la Expectativa | La Desviación de la Expectativa | La Desviación al Cuadrado |
| 0 | 0,25 | 4 | 0 – 4 = -4 | (-4)2 = 16 |
| 1 | 0,25 | 4 | 1 – 4 = -3 | (-3)2 = 9 |
| 7 | 0,25 | 4 | 7 – 4 = 3 | 32 = 9 |
| 8 | 0,25 | 4 | 8 – 4 = 4 | 42 = 16 |
| Total | 1 |
(0.25 x 16) + (0.25 x 9) + (0.25 x 9) + (0.25 x 16) = 12,5
La raíz cuadrada de 12.5 es 3.54.
Como esperábamos, el DesvEst de Distribución B es mayor que la de Distribución A.
Como esperábamos, el DesvEst de Distribución B es Mayor Que la de Distribución A.


