Para un mejor aprendizaje, se utiliza un ejemplo para introducir el concepto de cálculo desviación estándar.
En el país A se celebra todos los años un torneo de jugadores de Baloncesto para elegir al campeón de emboques desde media cancha.
Cada uno de los clubes de Baloncesto envía un representante al torneo. Cada participante lanza 10 veces desde media cancha. El ganador del Torneo (quien emboque más tiros a la cesta) recibe un premio de $1 millón, y su entrenador en el club también recibe la misma suma.
En el club de baloncesto “Glorias”, el entrenador elije a su representante de entre cuatro jugadores sobresalientes de la siguiente manera:
-
El hace que cada jugador pase cinco rondas de 10 lanzamientos de media cancha.
-
El elige el jugador con el promedio más alto en las cinco rondas.
La siguiente tabla muestra los resultados de las rondas de lanzamientos de los jugadores:
Tabla 3.14
| Jugador 1 | Jugador 2 | Jugador 3 | Jugador 4 | |
| Resultados de la ronda 1 | 1 emboque | 3 emboques | 6 emboques | 8 emboque |
| Resultados de la ronda 2 | 0 emboques | 2 emboque | 4 emboque | 2 emboque |
| Resultados de la ronda 3 | 6 emboques | 4 emboque | 6 emboques | 8 emboque |
| Resultados de la ronda 4 | 0 emboques | 0 emboque | 4 emboque | 1 emboque |
| Resultados de la ronda 5 | 6 emboques | 6 emboques | 5 emboque | 6 emboques |
| Total de emboques | 5 emboques | 15 emboque | 25 emboque | 25 emboque |
| Promedio por Ronda | 1 emboque | 3 emboque | 5 emboque | 5 emboque |
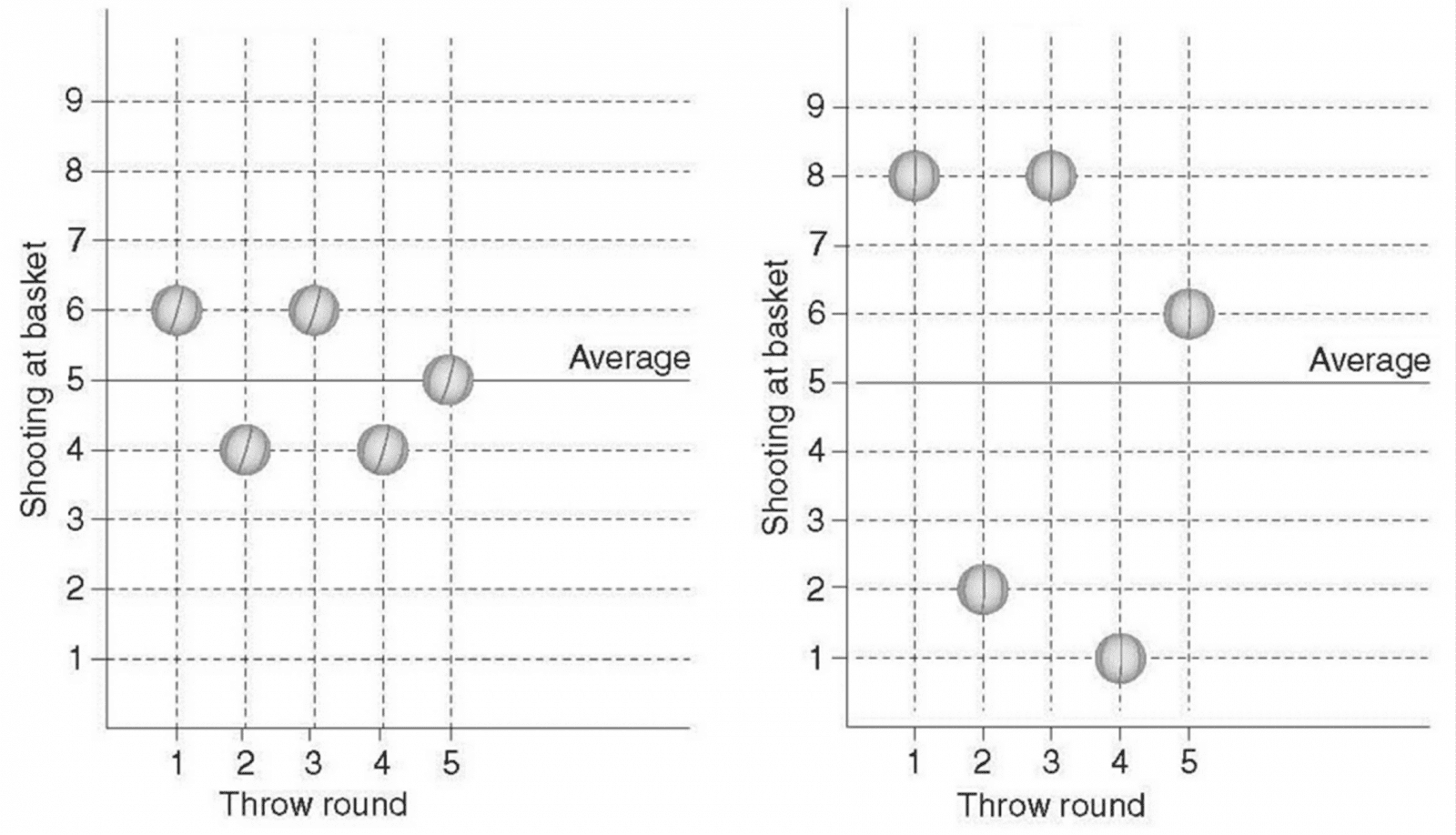
Los jugadores 3 y 4 embocaron el promedio más alto de cestos por ronda (5 cestos por ronda). El entrenador de Glorias tiene que elegir a uno de los dos y él le solicita a Ud. que lo ayude en la elección. El también le menciona dos datos importantes:
-
El ganador del torneo del año pasado tuvo un promedio de 4 emboques por ronda.
-
El entrenador ganará $1 millón si su representante gana.
De la observación de los resultados en la tabla parece razonable que elija al jugador no. 3, dado que la volatilidad (es decir, falta de consistencia) en el número de sus emboques de ronda a ronda es relativamente pequeña, y ella va a poner menos en peligro el premio del entrenador, en comparación a otros jugadores.
3 hubiera podido dar expresión a su presente capacidad en el torneo del año pasado, habría tenido una buena posibilidad de ganar el primer puesto – o por lo menos compartirlo, ya que en ninguna ronda embocó menos de 4 cestos. Si el jugador no. Por otro lado, el jugador no.4 acusa una variación más alta de ronda a ronda. Si él hubiese participado en el torneo del año pasado habría también una posibilidad de que embocase menos de 4 cestos por ronda.
La Volatilidad (en Emboques) se Interpreta como un Factor de Riesgo
A efectos de la explicación que sigue usaremos también la palabra inestabilidad como sinónimo de la palabra volatilidad. A continuación hacemos una comparación entre inestabilidad y volatilidad en 3 situaciones:
-
Inestabilidad = volatilidad.
-
Estabilidad completa = ausencia de volatilidad.
-
Mayor estabilidad = menor volatilidad.
Ante los ojos de la mayoría de las personas, la volatilidad en los emboques del jugador no. 4 pone más en peligro el premio del entrenador que la estabilidad del jugador no. 3 a pesar de que ambos ostentan la misma media de emboques. En el sector financiero, el riesgo está relacionado a la volatilidad. Más riesgo se atribuye a una mayor volatilidad.
Ejemplo:
Manuel compró acciones de dos bancos: A cambio de las acciones de cada banco él pagó $1,000 y en total invirtió $2,000. Al final de cada mes, las ganancias de sus inversiones en ese mes se le informe y registra los resultados en una tabla.
Los porcentajes de beneficio en cada mes se refieren al importe original de la inversión.
Por ejemplo, en el primer mes él ganó $10 en el Banco A (que es el 1% de $1,000) y en el Banco B ganó $30 (que equivalen al 3% de $1,000).
En el segundo mes, él ganó en el Banco A nuevamente $10 (1%), y en el Banco B perdió $20 (-2%). En el sexto mes él ganó en el Banco A nuevamente $10 (1%), y en el Banco B perdió $50 (-5%).
Tabla 3.15 –Datos de la Ganancia Mensual (en Porcentaje) para las Acciones Bancarias
| Mes | Acciones del Banco A | Acciones del Banco B |
| 1er mes | 1% | 3% |
| 2do mes | 1% | -2% |
| 3er mes | 1% | 5% |
| 4to mes | 1% | -3% |
| 5to mes | 1% | 8% |
| 6to mes | 1% | -5% |
| Ganancia promedio por Mes | 1% | 1% |
Los porcentajes de ganancia se refieren a la inversión original ($1,000 en acciones de cada uno de los bancos).
Al cabo de 6 meses Manuel calculó el beneficio medio de las acciones de cada banco y se sorprendió en descubrir que tuvo una ganancia promedio de 1% por mes (o $10) de las acciones de cada uno de los bancos. Sin embargo, cuando observamos la volatilidad de la ganancia de un mes al otro, se puede apreciar que la ganancia de las acciones del Banco A es muy estable mientras que los beneficios de las acciones del Banco B eran extremadamente volátiles. No hay estabilidad en el beneficio y por lo tanto no se puede «contar» con él.
En esta situación, en la cual las acciones de los dos bancos nos devengan el mismo promedio de beneficio mensual, preferiremos invertir en las acciones cuya volatilidad sea menor; es decir, cuya rentabilidad mensual sea más estable.
Una Medida de la Volatilidad
Volvamos al ejemplo del baloncesto. La elección del jugador no. 3 (y no el jugador no.4) en ese ejemplo, se hizo solamente en base a la apreciación visual. Empero, los economistas han desarrollado una «herramienta» más científica, asombrosamente simple, para examinar la variabilidad. Esa «herramienta» es conocida como la desviación estándar, y se la señala por medio de la letra griega σ.
Calculando la Desviación Estándar del Jugador no. 4
Demostrando el cálculo usando la Tabla.
-
Se introduce el número de cestas hechas en cada ronda – Columna 2. El promedio (5 canastas) se inserta en la fila 6. La letra M se utiliza habitualmente para referirse a la media.
-
Columna 3 – Llenaremos la columna a todo su largo con el valor de la media.
-
Columna 4 – Calcularemos en ella la diferencia entre el número de emboques en cada ronda (columna 2) y la media M de emboques (columna 3), renglón por renglón.
-
(-4)2 = 16]. Columna 5 – En cada renglón elevaremos al cuadrado (a la potencia 2) la diferencia de la columna 4 [Ej.; en el renglón 4: En el renglón 6 de esta columna se calcula la media de todos los resultados en esta columna (= 8.8).
-
Columna 6 representa la desviación estándar. Columna 6 – En el renglón 6 se calcula la raíz cuadrada de la media de los resultados de la columna 5 (= 8.8). El resultado obtenido es la desviación estándar (= 2.966).
El uso de la palabra “Distancia” en lugar de ”Diferencia”
En varias situaciones corresponde más utilizar el término “distancia del promedio” en lugar de “diferencia con respecto al promedio”.
Por ejemplo; cuando se mide la altura de niños es más adecuado usar la frase: la distancia entre los resultados y el promedio es 20 cm, en lugar de: “la diferencia entre los resultados y la media es 20 cm”.
Tabla 3.16
| No. de Ronda | Numero de Emboques por Ronda | Promedio de Emboques (M) | Cuadrado de la Diferencia | Diferencia entre el No. de Emboques y el Promedio | Raíz Cuadrada |
| Ronda 1 | 8 | 5 | 3 | 9 | |
| Ronda 2 | 2 | 5 | -3 | 9 | |
| Ronda 3 | 8 | 5 | 3 | 9 | |
| Ronda 4 | 1 | 5 | -4 | 16 | |
| Ronda 5 | 6 | 5 | 1 | 1 | |
| 5 promedio | 8,8 promedio | √8.8=2.966 Desviación Estándar |
Unidades de Medición para la Desviación Estándar
La desviación estándar se mide en las mismas unidades de medida de los datos.
-
Cuando los datos son las alturas de niños en cm, la desviación estándar se mide en cm.
-
Cuando los datos son el número de emboques al cesto – la desviación estándar se mide en número de emboques al cesto.
-
Cuando los datos son los de pescados en Kg, la desviación estándar se mide en Kg.


