平均数的含义

平均数是计算结果的一个简单数据。平均数是指用相同的单位衡量具有类似性质的一组数据的中间值（计算结果）。这组数据可以代表学校1年级孩子的成绩、10岁孩子的高度等，术语“平均数”更精确的定义将会在本章的后面部分出现。

如何计算平均数

这里列出了三种计算下例中10个4年级学生数学测验平均分数的办法。

方法一:把所有的学生人数相加，然后除以学生数

表 3.1 列出了每个学生的测验成绩。

表 3.1

学生 (以姓氏排序)	成绩 (分数)
学生 1	90 分
学生 2	80 分
学生 3	70 分
学生 4	90 分
学生 5	80 分
学生 6	70 分
学生 7	80 分
学生 8	70 分
学生 9	70 分
学生 10	70 分
总分	770 分
平均分

77 分 = 770 分/10个学生为了计算平均值，我们将所有学生的分数相加，得到的总分为770分，然后除以学生人数，得到77分。平均成绩为77分。

平均数更精确的定义

我们把该组学生的总分（770分）称为“该组学生的原始总分”。平均数是这样一个数据，当所有学生的分数都相等并等于它时，那么分数的总和将等于（该组学生的）原始总分。

即77 (平均数) x 10 = 770 分。

方法二:通过每个学生对平均数的贡献来计算

正如我们将马上看到的，每个学生的分数对平均数都有一定的贡献分数。有两个因素影响到贡献分数。

1. I. 该学生的分数 – 分数越高，对平均数的贡献越大。

2. II. 该学生在班上的相对比例 (稍后解释)。

相对比例是指学生分数在班上总分数中所占的比例。

• 在由10个学生组成的班级中，每个学生占班级总人数的1/10，或 10%。

• 在由2个学生组成的班级中，每个学生占班级总人数的1/2，或 50%。

• 在由1个学生组成的班级中，每个学生占班级总人数的1，或100%。

学生的相对比例越大，其对平均数的贡献越大。

经济学者不使用相对比例，而是用权重进行表示。此后我们将（在多数情形中）使用后一个术语。

说明分为两部分:

• A部分 是10个学生中每个学生的分数。

• B 部分是每个学生对平均数的贡献及其计算方法。

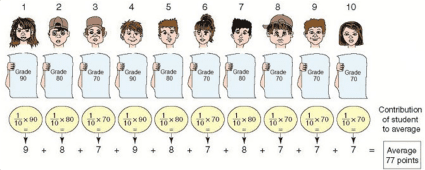
从图表中可以看出,学生1为平均分贡献了9分。他所作出的贡献是他的分数(90分)乘以他的班级权重(10%)。学生 2为平均分贡献了8分(他的分数是80 分, 权重是10%)，以此类推至第10个学生。

插图 3.1

方法三 ：通过将相同分数的学生分组来计算

此方法很普遍，在多数情形中也最简单。我们按照分数对学生进行分组，以便计算。

 

插图 3.2

 

有两个因素影响到该组对平均数的贡献:

• I. 该组分数 – 分数越高，对平均数的贡献越大。

• II. 该组权重 – 该组学生的权重是该组所有学生的总权重。

本例中，每个学生的权重是10%（这样三个学生的权重就是30%，五个学生的权重是50%）。

在插图3.2中可以看到:

• 1组向平均分贡献了18分。

• 2组向平均分贡献了24分。

• 3组向平均分贡献了35分。

三个组总共贡献了77分，即平均分数。

下表列出了这些数据

表 3.2

编组	每组的数据观察 (分数)	每组人数	每组权重	每组对平均数的贡献
1	2	3	4	2= 5X 4
第 1组	90 分	2	20%	18 分
第 2组	80 分	3	30%	24 分
第 3组	70 分	5	50%	35 分
总计		10	100%	77 分(平均数)