Los gráficos circulares

Tratamiento del Género de los Empleados

Cuando el estudiante comienza a investigar el género de los empleados, él compila una tabla como la siguiente:

En esta tabla, el género es la variable de la investigación. ¿Por qué variable? Porque el género es una característica que no es constante en todos los empleados; esta varía de un empleado a otro. Un empleado puede ser hombre (masculino) o mujer (femenino), es decir, la variable de género puede recibir dos valores: “Masculino” o “Femenino”. La frecuencia relativa de cada valor en porcentajes aparece en la tercera columna: La frecuencia de cada valor aparece en la segunda columna: el número de hombres (masculino) en la oficina aparece opuesto al valor “masculino” y el número de mujeres (femenino) en la oficina aparece opuesto al valor “femenino”.

La frecuencia relativa de cada valor en porcentajes aparece en la tercera columna: El porcentaje de empleados hombres (masculino) aparece en la fila de “masculino” y el porcentaje de mujeres (femenino) aparece en la fila de “femenino”. Según esta tabla, 8 hombres trabajan en la oficina constituyendo el 27% de todos los empleados en la oficina, y 22 mujeres trabajan en la oficina, constituyendo el 73% de todos los empleados en la oficina. Es necesario agregar otra fila, la última fila, para una tabla de frecuencia en la cual aparecen las sumas de las columnas.

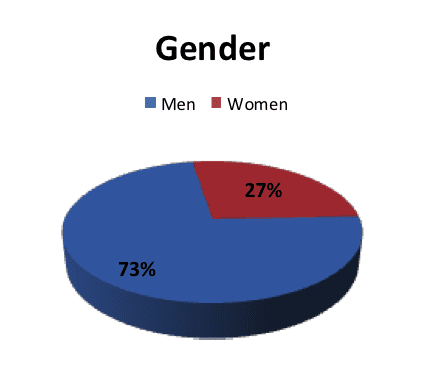
Notamos que en el caso del género, el orden de enumeración en la tabla no tiene importancia. El estudiante puede haber presentado a las mujeres en la primera fila y a los hombres en la segunda. La tabla de frecuencia puede ser presentada visualmente al usar un gráfico circular o diagrama de pastel:

El diagrama es llamado un diagrama de pastel debido a su forma redonda. Cada valor (masculino y femenino) recibe un área en el pastel correspondiente a su frecuencia relativa. En nuestro caso, los hombres reciben el 27% del área (podemos ver que los hombres reciben un poco más de un cuarto del pastel) y las mujeres reciben el 73% restante. El diagrama y las tablas responden la pregunta de cuál es la distribución de género entre los empleados en la oficina. La distribución es la manera en la cual los empleados en la oficina están divididos entre hombres y mujeres.

Tratamiento del Estatus en el Trabajo de los Empleados

El mismo proceso de organización de datos puede efectuarse sobre la sección del estado civil, o, en otras palabras, cuando revisemos la distribución del estado civil de los empleados de la empresa. El estado civil también es una variable, sin tener importancia su orden. La variable «estado civil» puede recibir los valores «divorciado/a», «casado/a», «soltero/a» y «viudo/a», y cómo ya mencionamos anteriormente, el orden entre ellos no tiene importancia alguna. El orden entre ellos es importante.

Preparemos entonces, una tabla de frecuencia de la siguiente manera:

1. Escribiremos estos valores (divorciado/a, casado/a, soltero/a, viudo/a) en la primer columna en cualquier orden por favor – esta es la columna del valor. Esta es la columna de valor.
2. Escribiremos la frecuencia de cada valor (el número de empleados) en la segunda columna – esta es la columna de la frecuencia. Esta es la columna de frecuencia.
3. Para cada valor calcularemos la proporción que constituye del total de la cantidad de datos.
4. Escribiremos los resultados del cálculo en (3) de la tercera columna – esta es la columna de la frecuencia relativa. Esta es la columna de frecuencia relativa.
5. Las primeras dos columnas:

Calculamos las frecuencias relativas:

Para los solteros/as: 6/30 = 20%

Para los viudos/as: 1/30 = 3,33%

Para los divorciados/as: 4/30 = 13,33%

Para los casados/as: 19/30 = 63,33%

La frecuencia para el último grupo (casados/as) también puede ser calculada al completar la suma a 100%. La suma de los porcentajes de todos los primeros grupos es de 20% + 3,33 % + 13,33 % = 36,66 %.

Con el fin de total del 100 %, el porcentaje del último grupo debe ser 100% – 36,66 % = 63,34 %

Dados los problemas de redondeo, existe una pequeña diferencia entre los dos cálculos: Obtuvimos 63.33% en el primer cálculo y 63.34% en el segundo. Preferimos el segundo método para que todas las frecuencias relativas sumen 100%.

Ahora procederemos a agregar éstos resultados cómo una tercera columna en la tabla, y recibiremos una tabla de frecuencias:

Después que hemos organizado los datos en una tabla, podemos presentar la distribución del estado civil usando un diagrama de pastel.

Esta vez, el pastel tendrá cuatro “tajadas”.