La diferencia entre el valor recibido en la muestra más alto y el más bajo es el rango de la muestra. De nuevo, utilizaremos las tres muestras que mostramos anteriormente:
Muestra A: 7, 7, 7, 7, 7, 7.
Muestra B: 10, 10, 7, 7, 7, 4.
Muestra C: 8, 7, 7, 7, 7, 7.
Recordemos que las medidas de centralidad de estas muestras son idénticas. ¿Cuál es el rango de cada muestra? En la Muestra A, el valor más alto es 7 y el valor más bajo es 7, así que el rango es 0 (7 – 7 = 0).
Esta es una indicación que la muestra está centralizada, y en efecto carece de dispersión en lo absoluto. El rango de la Muestra B es 6, porque el valor más alto es 10 y el más bajo es 4 (10 – 4 = 6). En la Muestra C, el valor más alto es 8 y el más bajo es 6, así que el rango es 2 (8 – 6 = 2).
Por lo tanto, la Muestra B es más dispersa que la Muestra C y ambas son más dispersas que la Muestra A.
¿Es el Rango una Medida de Dispersión?
Observe los siguientes ejemplos:
Muestra A: 8, 7, 6, 4, 3, 2.
Muestra B: 5, 5, 5, 5, 5, 5.
El rango de ambas muestras es 8, porque el valor más alto en ambas muestras es 9 y el más bajo es 1 (9 – 1 = 8).
Al mismo tiempo, es fácil ver que la Muestra A está ampliamente dispersa entre 1 y 9, mientras que en la Muestra B los valores 1 y 9 son prácticamente son poco frecuentes, mientras que los otros valores en la muestra son 5, lo que significa que la muestra está concentrada.
Vamos a examinar estas muestras con un palo diagrama.
Los diagramas de líneas para las muestras son de la siguiente manera:
MUESTRA A MUESTRA B
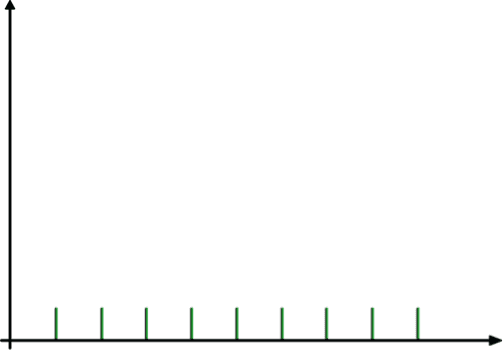
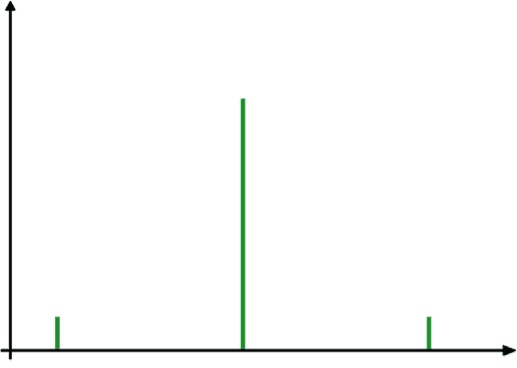
Por lo tanto se deduce que el rango no es una medida de dispersión suficiente; se necesita otra medida. Los estadistas han desarrollado una “herramienta” científica simple para examinar el grado de una dispersión. Esta “herramienta” es llamada la desviación estándar, denotada por la letra griega σ (una sigma pequeña).


