Usualmente no obtendremos una curva normal clara y simétrica en las muestras que tomemos. En la mayoría de los casos, la curva solamente será similar a una campana pero no mucho.
La distribución de la probabilidad que recibimos es denominada la distribución de muestra.
Por ejemplo, si medimos el peso de los peces en el Lago Michigan, podríamos obtener una distribución de probabilidad como la del ejemplo.

Calculo de las Probabilidades de una Distribución de Probabilidad Normal que está en la Forma de una Curva Normal
La estadística aún no ha encontrado una manera de calcular las probabilidades para una distribución de probabilidad normal basada en una muestra que no es una curva normal exacta, es decir, una curva en forma de campana completamente simétrica. En estos casos la solución es usar una curva normal que sea lo más cercana a la distribución de muestra. Utilizaremos esta curva normal para hacer los cálculos de la probabilidad.
Las probabilidades que obtenemos según la curva normal obviamente solo serán una aproximación (a veces a grandes rasgos) de las probabilidades que hubiésemos obtenido de la distribución de muestra, donde hubiese una manera de hacer el cálculo.
Mientras más experimentado y profesional sea el estadista, mejor podrá hacer uso del significado de los resultados aproximados y estimar el nivel de error que se haya creado.
Mientras más general y aproximada sea la perspectiva que queremos derivar de los datos, menor será la importancia de la exactitud, y aún más si los datos aproximados nos satisfacen.
Calculo de las Probabilidades de una Curva Normal Cualquiera
La comprensión de la Probabilidad de curva de distribución normal
Ejemplo:
Nos preguntamos la siguiente pregunta: Nos hacemos la siguiente pregunta: si elegimos al azar una persona de una multitud que celebra el Día de la Independencia, ¿Cuál es la probabilidad que su estatura este entre los 150 y 170 centímetros?
Asumimos que, según una muestra que hemos obtenido, la multitud de personas tienen la distribución de una curva normal (la curva normal del ejemplo) la cual es extremadamente cercana a la curva normal (la curva exacta) como se presenta en el Diagrama A, en el cual μ = 167 centímetros y σ = 2 centímetros. = 2 centímetros. Realmente, nos interesa calcular las probabilidades que un suceso específico ocurra.
Cada Persona cuya Estatura esté entre 150 y 170 Centímetros
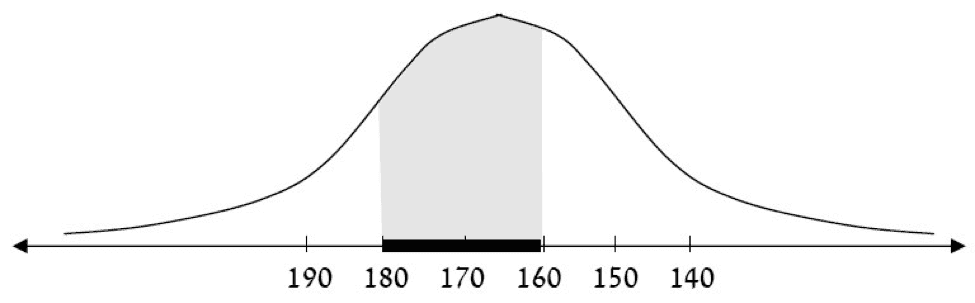
Marcaremos este evento en el eje de los números con una franja negra que empieza a los 150 centímetros y termina en los 170 centímetros.
La probabilidad que este suceso ocurra es el área bajo la curva y sobre la franja.
El área relevante para el evento siempre es menor a 100%, dado que al área total bajo la campana es igual a 100%.
Diagrama