Cómo calcular áreas bajo la curva normal
Los matemáticos han desarrollado una tabla llamada la tabla de la probabilidad estándar, o para ser breves, la distribución de probabilidad estándar.
distribución de probabilidad. Podemos usar esta tabla para hacer cálculos.
Información Preliminar – la Distribución de la Probabilidad Normal Estándar
La Curva Estándar
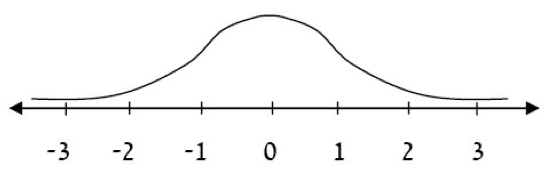
Hemos visto que hay un número infinito de formas que representan curvas (forma de campana) normales.
Una de ellas tiene las siguientes características:
- Su promedio es 0,
- Su desviación estándar es 1.
Una curva con estas características es denominada la curva estándar.
La tabla de distribución de probabilidad estándar puede calcular las áreas únicamente bajo la curva estándar. Afortunadamente, como veremos después, cualquier curva normal se puede convertir a una curva estándar.
Dicha conversión es posible porque todas las curvas tienen la misma área bajo ellas (=1).
Dado que la tabla se puede utilizar para calcular cualquier área bajo la curva estándar, también es posible calcular automáticamente cualquier área en cualquier otra curva normal, que llamaremos la curva objetivo. Dedicaremos los siguientes sub-capítulos a la curva estándar.
Características de la Curva Normal Estándar
Como se mencionó anteriormente, la curva estándar es una distribución de probabilidad normal con expectativa = 0 y desviación estándar =1.
Esto significa que la campana tiene su pico sobre 0 en el eje X, y el grado de su convexidad corresponde a una desviación estándar de 1. Las unidades en el eje X están en desviaciones estándar.
Ellos varían entre 3 desviaciones estándar a la derecha de 0 y 3 desviaciones estándar a la izquierda de 0.
Recordatorio de las características de la curva normal
Pregunta: ¿Cuál es la probabilidad de obtener valores menores que 0?
La respuesta es 0.5.
Explicación: sLa curva en forma de campana es simétrica alrededor de 0, y el área bajo la curva asciende a 1.
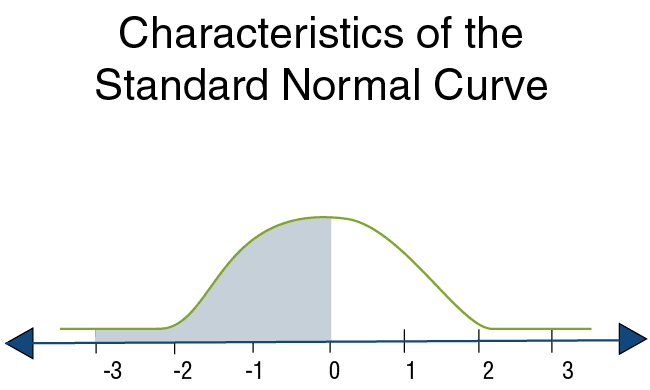
Por lo tanto, el área bajo la curva a la izquierda de 9 es exactamente la mitad del área bajo la curva, es decir, 0.5.
Pregunta:
¿Cuál es la probabilidad de obtener valores mayores que 0? 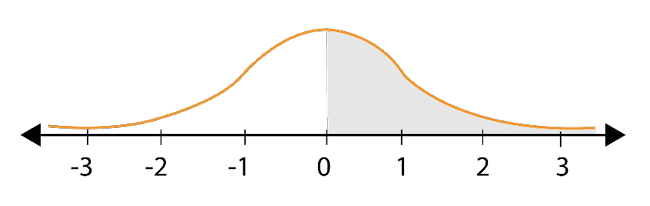
La respuesta es 0.5.


