De nuevo consideraremos los dos sucesos que ya hemos visto:
Suceso A – extraer una pelota con rayas.
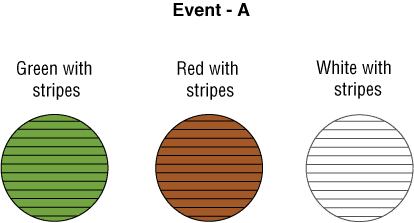
Suceso B – extraer una pelota verde.
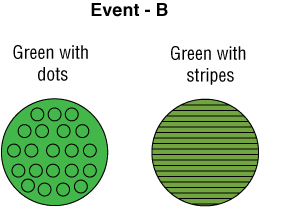
¿Cuál es la probabilidad que al menos uno de estos dos sucesos ocurra?
Hemos encontrado esto para usted.
Podemos unir estos sucesos en un solo suceso:

El tamaño del evento unido es 4.
El tamaño del espacio de la muestra es 5 (dado que hay cinco pelotas en el contenedor). Por lo tanto, la probabilidad que estamos buscando es 4/5.
El Cálculo Cuando los Sucesos son Mutuamente Excluyentes
Consideraremos los dos sucesos mutuamente excluyentes:
Suceso A – extraer una pelota con rayas.

Suceso B – extraer una pelota verde con puntos.
Verde con Puntos
Aquí, también podemos unir los sucesos en un solo suceso:

Llegamos a la conclusión que la probabilidad que ocurra cualquier suceso (A o B) es 4/5.
(Explicación: 4 pelotas (de un total de 5) pueden causar que el evento unido ocurra).
Sin embargo, debido a que los eventos son mutuamente excluyentes, podemos usar un método diferente:
Paso 1: Calculamos la probabilidad del Suceso A, y obtenemos 3/5 (Explicación: 3 pelotas [de un total de 5] puede causar que el Suceso A ocurra).
Paso 2: Calcularemos la probabilidad del Suceso B y obtenemos 1/5 (Explicación 1 pelota [de un total de 5] puede causar que el Suceso B ocurra).
Paso 3: Sumamos estas dos probabilidades (Paso 1 y Paso 2) y obtenemos 4/5.
Eventos complementarios – Ejemplo y explicación
Utilizaremos de nuevo los dos sucesos:
-
Suceso A – extraer una pelota con rayas:
-
Suceso B – extraer una pelota verde con puntos:
En este caso, también podemos calcular la probabilidad que uno de ellos ocurrirá al usar sucesos complementarios.
Solamente hay una pelota (roja con puntos) cuya extracción no causaría ni el Suceso A ni el Suceso B. Por lo tanto, el retirar una pelota roja con puntos es un suceso complementario para la unión de los Sucesos A y B. La probabilidad de retirar una sola pelota es de 1/5. El retirar cualquier otra pelota debe causar que los Sucesos A o B ocurran.
Por lo tanto, la probabilidad que ocurra cualquier Suceso (A o B) es 1 – 1/5 = 4/5.


