Porque las Medidas de Centralidad son Insuficientes para Describir una Distribución
Consideraremos tres muestras de datos como listas de valores (por ejemplo, podemos asumir que son notas de estudiantes):
Muestra A: 7, 7, 7, 7, 7, 7.
Muestra B: 10, 10, 7, 7, 7, 4.
Muestra C: 8, 7, 7, 7, 7, 7.
Estas tres muestras tienen la misma moda (7), la misma media (7) y el mismo promedio (7). ¿Entonces cuál es la diferencia entre estas muestras? Es fácil ver que no tienen características idénticas. La diferencia es en la forma en que están dispersas.
Muestra A No está dispersa en lo absoluto, está concentrada en un solo punto.
Muestra B es el más disperso de las tres muestras. Muestra B Es la más dispersa de las tres muestras, tiene valores que están distantes del centro y estos valores aparecen en una cantidad significativa en la muestra.
Muestra C Tiene una dispersión media, los valores están enfocados alrededor del centro.
Veremos Otros Ejemplos:
Es posible tener muestras con diferentes centros pero con la misma dispersión. Demostraremos esto utilizando variables continuas.
Haremos una muestra de la altura (en centímetros) de los residentes de cierta ciudad. Se hizo una muestra de 100 personas y a continuación se presentan los resultados obtenidos:
| Los valores de altura) | La frecuencia | La Frecuencia Relativa | El Ancho de la División | La Densidad |
| 140-150 | 10 | 10% | 10 | 1 |
| 150-160 | 20 | 20% | 10 | 2 |
| 160-170 | 40 | 40% | 10 | 4 |
| 170-180 | 20 | 20% | 10 | 2 |
| 180-190 | 10 | 10% | 10 | 1 |
| Total | 100 | 100% |
En otra ciudad, hacemos una muestra del peso (en kilogramos) de los residentes. La cantidad de 500 muestras. A continuación se presenta la tabla de frecuencia:
| Los valores (peso) | La frecuencia | La Frecuencia Relativa | El Ancho de la División | La Densidad |
| 50-60 | 50 | 10% | 10 | 1 |
| 60-70 | 100 | 20% | 10 | 2 |
| 70-80 | 200 | 40% | 10 | 4 |
| 80-90 | 100 | 20% | 10 | 2 |
| 90-100 | 50 | 10% | 10 | 1 |
| Total | 500 | 100% |
Examinaremos los histogramas de las dos muestras:
El histograma de altura y peso:
Histograma
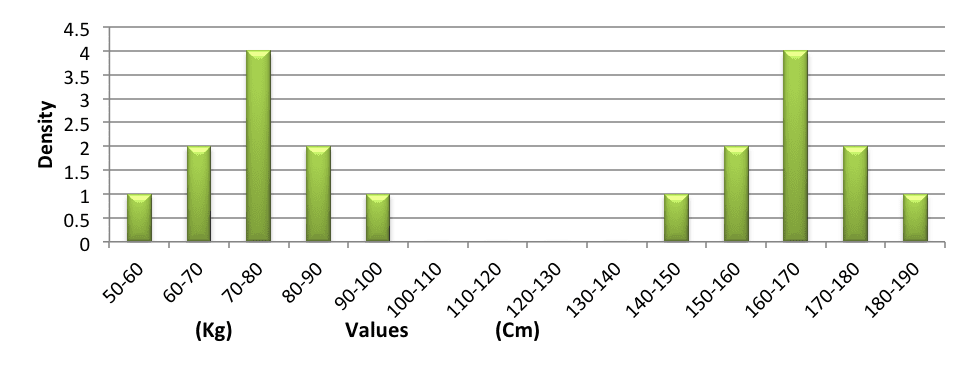
No es difícil percibir que la dispersión es idéntica, pero los valores del muestreo son distintos: 165 en el muestreo de las estaturas, y 75 en el muestreo de los pesos.


