Un promedio es un número único que resulta de un cálculo. Un promedio es un único numero (el resultado del cálculo) que indica algo como una medida media de un grupo de datos o caracteres similares que son medidos en la misma unidad. El grupo de datos pueden ser notas de niños en 1er año en la escuela, la altura de un niño de 10 años, etc. Una definición más exacta del término “promedio” será presentada más adelante.
Como Calcular un Promedio
Presentaremos tres métodos de calcular un promedio en un ejemplo que involucra las notas de 10 niños de 4to año en un examen de aritmética.
Primer Método: Sumar las Notas y Dividir el Total entre el Número de Alumnos
La Tabla 3.1 detalla las notas de los alumnos en el examen.
Tabla 3.1
|
Lista de Alumnos |
Notas |
|
Alumno no. 1 |
90 puntos |
|
Alumno no. 2 |
80 puntos |
|
Alumno no. 3 |
70 puntos |
|
Alumno no. 4 |
90 puntos |
|
Alumno no. 5 |
80 puntos |
|
Alumno no. 6 |
70 puntos |
|
Alumno no. 7 |
80 puntos |
|
Alumno no. 8 |
70 puntos |
|
Alumno no. 9 |
70 puntos |
|
Alumno no. 10 |
70 puntos |
|
Total de las Notas |
770 puntos |
|
Promedio |
|
Para poder calcular el promedio, primero calculamos el total de la suma de todas las notas de los alumnos. El total es 770 puntos y luego lo dividimos por el número de alumnos en el grupo y obtenemos 77 puntos. El promedio es de 77 puntos.
Una Definición Más Exacta del Promedio
Nos referiremos al total de las notas del grupo (770 puntos) como el “total original de las notas del grupo”. El promedio es el número que, so todas las notas fuesen idénticas e iguales a él, entonces el total seria la misma cantidad que el total original (de las notas del grupo).
Esto significa que 77 (el promedio) por 10 = 770 puntos.
Segundo Método: Usando el Aporte de Cada Alumno al Promedio
Como veremos a continuación, cada alumno contribuye con un número de puntos al promedio. Dos factores afectan el tamaño de la contribución.
-
Su Nota – mientras más alta es la nota, mayor es su contribución al promedio.
-
Su Proporción Relativa del Salón (se explicará más tarde).
La expresión su Proporción Relativa indica la proporción del alumno del total del número de alumnos en la clase.
-
En una clase en la que hay 10 alumnos, cada alumno constituye 1/10 o 10% del total de alumnos.
-
En una clase en la que hay 2 alumnos, cada alumno constituye 1/2 o 50% del total de alumnos.
-
En una clase en la que hay 1 alumno, cada alumno constituye 1 o 100% del total de alumnos.
A medida que la Proporción Relativa del Alumno es más grande, mayor es su aporte a al promedio.
En lugar de la expresión Su Proporción Relativa, los economistas utilizan el término peso. De ahora en adelante, utilizaremos el segundo término (en la mayoría de los casos).
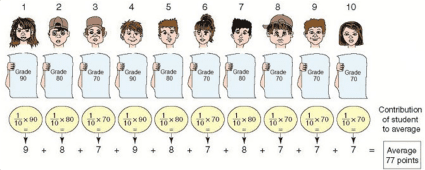
La ilustración 3.1 demuestra la contribución de cada alumno al promedio. La ilustración está dividida en dos partes:
-
Parte A muestra a cada uno de los 10 alumnos con la nota que recibió.
-
Parte B muestra la contribución de cada alumno en el promedio y como fue calculado.
En la ilustración se puede observar que el alumno no. 1 aporta 9 puntos a la media. Su aporte se calcula multiplicando a su nota (90 puntos) por su peso en la clase (10%). El alumno no. 2 aporta 8 puntos a la media (su nota es de 80 puntos y su peso es 10%), y así sucesivamente hasta el alumno no. 10.
Ilustración 3.1
Tercer método: Tercer Método – Usando Grupos de Alumnos con la Misma Nota
Este método es el más popular y en varios casos también el más simple. A efectos del cálculo se ordena a los alumnos de la clase en grupos de acuerdo a la nota que recibieron.
Ilustración 3.2

Dos factores afectan el tamaño de la contribución de cada grupo:
-
La Nota del Grupo – cuanto más alta es la nota, más alto es el aporte del grupo al promedio.
-
El peso del Grupo – el peso del grupo es igual a la suma de los de todos los alumnos en el grupo.
En nuestro ejemplo , el peso de cada alumno es 10%. (y de esa manera, el peso de 3 alumnos es 30% y el de 5 alumnos es 50%).
En la ilustración, se puede ver que:
-
El grupo 1 aporta 18 puntos al promedio.
-
El grupo 2 aporta 24 puntos al promedio.
-
El grupo 3 aporta 35 puntos al promedio.
Y en total, los 3 grupos aportan, que es el promedio.
Organizando los Datos en la Tabla
Tabla 3.2
|
Numeración del Grupo |
Datos de la Muestra del Grupo (ganancias de las barberías) |
Número de Individuos en Cada Grupo |
El peso del grupo |
La Contribución del Grupo al Promedio |
|
1 |
2 |
3 |
4 |
∑2,3,4 |
|
Grupo 1 |
90 pts. |
2 |
20% |
18 pts. |
|
Grupo 2 |
80 pts. |
3 |
30% |
24 pts. |
|
Grupo 3 |
70 pts. |
5 |
50% |
35 pts. |
|
Total |
|
10 |
100% |
77 pts. (el promedio) |


