José tiene acciones. La ganancia anual sobre estas acciones tiene una probabilidad normal con una expectativa de 9.6% y una desviación estándar de 8%. Esta expectativa de 9.6% no garantiza una ganancia segura de 9.6% cada año.
La distribución de la probabilidad de la ganancia puede ser representada por una campana:
Diagrama
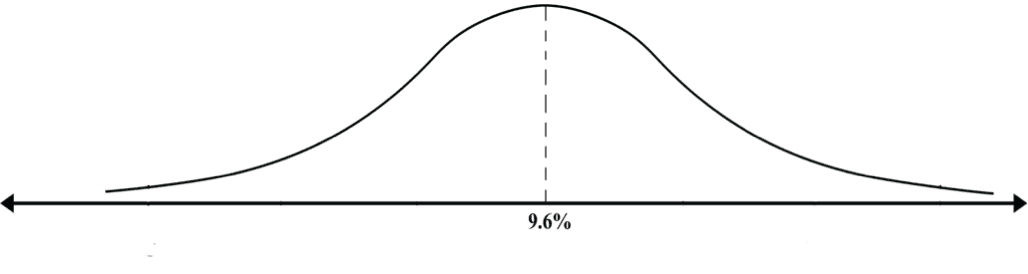
¿Cuáles son las probabilidades que José obtenga ganancia este año?
Obtener ganancia significa una ganancia mayor que cero (una perdida es en realidad una ganancia negativa). Estamos preguntando cuales son las posibilidades que la ganancia en este año sea mayor a 0. Realmente estamos buscando el área marcada en el siguiente diagrama:
Diagrama
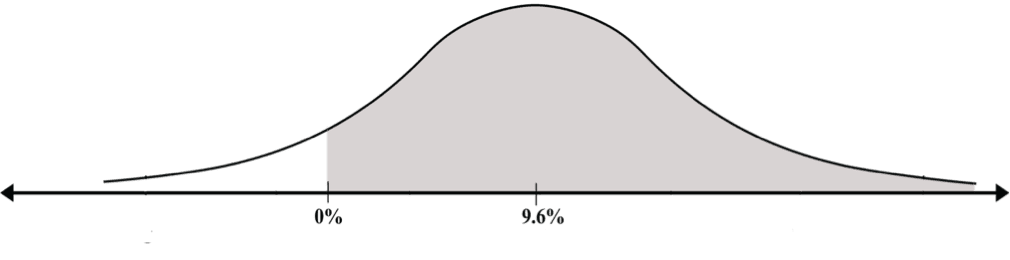
Debemos encontrar la unidad estándar.
La unidad estándar de cero es (0-9.6)/8 = -9.6/8 = -1.2. Agregamos esto al diagrama en la fila de las unidades estándar.
Diagrama
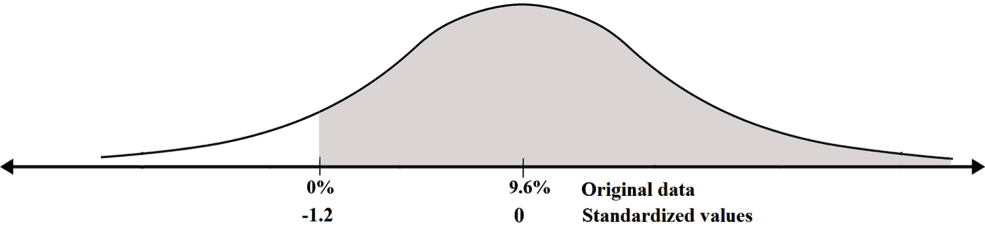
Hemos traducido la pregunta original a la siguiente pregunta: ¿Cuál es el área a la derecha de -1.2 en la distribución estándar?
Para poder responder esta pregunta debemos ver la tabla. El área a la izquierda de -1.2 es -0.1151, así que el área a la derecha de -1.2 es 1 – 0.1151 = 0.8849. Por lo tanto, las posibilidades que José obtenga ganancia este año son 0.8849 (de 1). Es decir, las posibilidades que José obtenga ganancia son 88.49%.


