Proporcionaremos un ejemplo para acompañar la explicación. Este ejemplo se refiere a la estatura de niños de diez años.
- Una Variable Continua – La distribución normal es una distribución de una variable continua, que puede ser adjudicada a cualquier valor numérico: números enteros (101 centímetros), números con fracciones (101.25), números positivos, y números negativos (nuestro ejemplo no incluye números negativos).
- La Estatura Refleja la Probabilidad – La altura de la curva sobre cada uno de los valores refleja la posibilidad de recibir ése valor/número, en relación a los otros valores. Mientras más nos alejamos del centro (hacia la derecha y la izquierda), ésta posibilidad disminuye gradualmente.
- El Centro es la Expectativa –El resultado del centro es el promedio y la probabilidad de en el más alto de los otros números. La razón por la cual el resultado del centro es el promedio es que la curva es simetría alrededor del centro. Esto significa que por cada resultado a la derecha del centro, lo cual contribuye a aumentar el promedio, existe un resultado que está a la misma distancia de la izquierda con la misma posibilidad de ser obtenido, lo cual contribuye al mismo grado de disminuir el promedio.
- Simetría – La distribución normal es simétrica alrededor del promedio. Esto significa que la posibilidad de recibir un resultado que es mayor que 10 del valor promedio, es igual a la posibilidad de recibir un resultado que es menor que 10 del mismo valor promedio.
- Las probabilidades son conocidas de antemano.
Las probabilidades (= superficies de la curva) a ambos lados del valor promedio, se dispersan cómo se presenta a continuación:
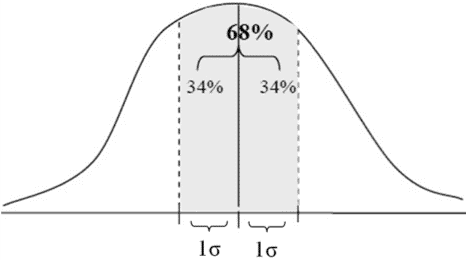
- Cada área sobre el segmento (sobre el eje X) con un largo de una desviación estándar (1δ) del promedio, una al lado derecho y otra al lado izquierdo, totaliza 34% del área bajo la curva normal. El are sobre un segmento con un largo de dos desviaciones estándar de ambos lados del promedio (de 1 desviación estándar la izquierda del promedio a 1 desviación estándar del
Diagrama
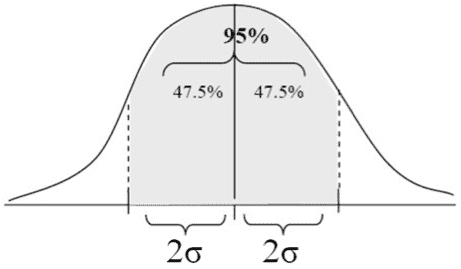
- Cada área sobre el segmento con un largo de dos desviaciones estándar (2σ) del promedio, una al lado derecho y otra al izquierdo, totaliza 47.5% del área total bajo la curva normal. El área sobre un segmento con el largo de las desviaciones estándar de ambos lados del promedio (de 2 desviaciones estándar a la izquierda del promedio a dos desviaciones estándar del lado derecho) por lo tanto totaliza 95% del área total bajo la curva normal.
Diagrama
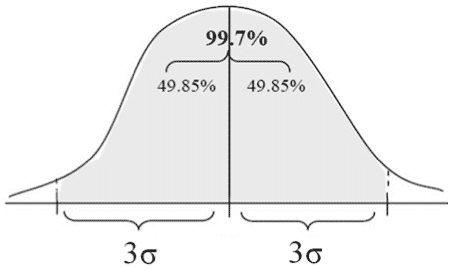
- Cada área sobre el segmento con un largo de 3 desviaciones estándar (3σ) del promedio, una a la derecha y otra a la izquierda, totaliza 49.85% del área total bajo la curva normal. El área sobre un segmento con un largo de 6 desviaciones estándar en ambos lados del promedio (de 3 desviaciones estándar a la izquierda del promedio a 3 desviaciones estándar a la derecha) por lo tanto totaliza alrededor de 99.7% del área total bajo la curva normal.
Diagrama
Marcado intervalos en el eje X
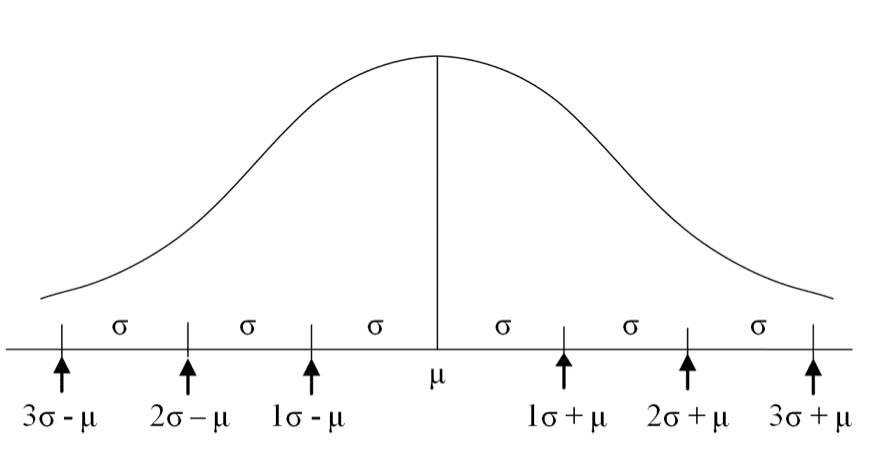
Se denota el promedio por la letra griega μ (mu).
Se denota la desviación estándar por la letra griega σ (sigma).
Un punto de 1 desviación estándar a la derecha del promedio se denota por μ + 1σ.
Un punto de 1 desviación estándar a la derecha del promedio se denota por μ + 1σ.
La distancia entre estos dos puntos se denota por μ +/- Xσ.
En General
Un punto de X desviaciones estándar a la derecha del promedio se denota por μ + Xσ.
Un punto de X desviaciones estándar a la izquierda del promedio se denota por μ – Xσ.
La distancia entre estos dos puntos se denota por μ +/- Xσ.
a la derecha y una a la izquierda) asciende a 47,5% de la superficie total dentro de la curva normal.
El área sobre un segmento con el largo de las desviaciones estándar de ambos lados del promedio (de 2 desviaciones estándar a la izquierda del promedio a dos desviaciones estándar del lado derecho) por lo tanto totaliza 95% del área total bajo la curva normal.
3 Cada área sobre el segmento con un largo de 3 desviaciones estándar (3σ) del promedio, una a la derecha y otra a la izquierda, totaliza 49.85% del área total bajo la curva normal.
El área sobre un segmento con un largo de 6 desviaciones estándar en ambos lados del promedio (de 3 desviaciones estándar a la izquierda del promedio a 3 desviaciones estándar a la derecha) por lo tanto totaliza alrededor de 99.7% del área total bajo la curva normal.
Se denota el promedio por la letra griega μ (mu). (mu).
Se denota la desviación estándar por la letra griega σ (sigma). (sigma).
Un punto de 1 desviación estándar a la derecha del promedio se denota por μ + 1σ. 1
Un punto de 1 desviación estándar a la derecha del promedio se denota por μ + 1σ. 1
La distancia entre estos dos puntos se denota por μ +/- Xσ. –
El Significado de las Áreas bajo la Curva
Como se ha mencionado anteriormente, las áreas bajo la curva representan las probabilidades. En nuestro ejemplo, la probabilidad de encontrar un niño cuya altura está entre el segmento μ – σ y μ + σ es 68%.
En otras palabras:
Por cada 1,000 niños que vemos en la calle, la estatura de 680 de ellos (68%) estará en el segmento entre μ – δ y μ + δ.
Por lo tanto:
De cada 1,000 niños que vemos en la calle, la estatura de 950 de ellos (95%) estará en el segmento entre μ – 2σ y μ + 2σ, y la estatura de 997 de ellos (99.7%) estará en el segmento entre μ – 3σ y μ + 3σ.
Solamente 3 de cada 1,000 niños estarán fuera del segmento entre μ – 3σ y μ + 3σ.





