Joe holds shares. The annual profit on these shares has a normal probability with an expectation of 9.6% and a standard deviation of 8%. This expectation of 9.6% profit does not guarantee a 9.6% profit each year.
The probability distribution of the profit can be represented by a bell-shaped curve:
Diagram
What are the chances that Joe will make a profit this year?
Earning a profit means obtaining a profit larger than zero (i.e., a loss is actually a negative profit). What are the chances that the profit this year will be greater than 0. We are actually looking for the area shaded in the following diagram:
Diagram
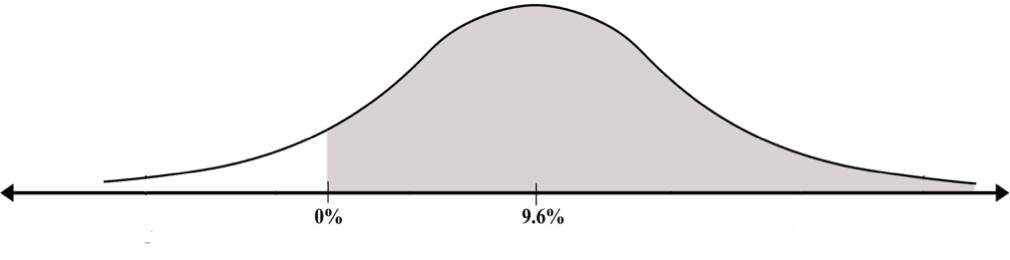
We must first find the standard unit.
The standard unit of zero is (0-9.6)/8 = -9.6/8 = -1.2. We add this to the diagram in the standard units row
Diagram
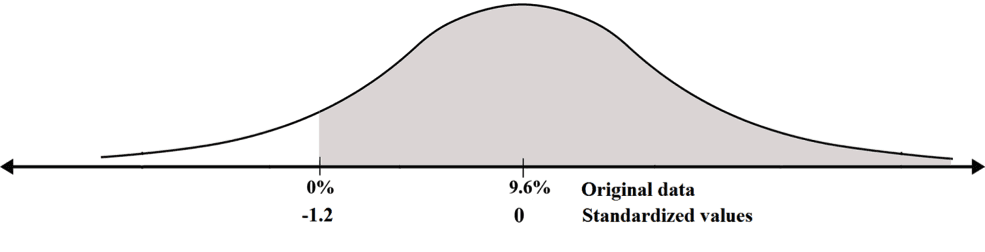
We have reiterated the original question as follows: What is the area to the right of –1.2 in the standard probability distribution?
In order to answer this question, we must examine the table. The area to the left of -1.2 is -0.1151, so the area to the right of -1.2 is 1 – 0.1151 = 0.8849. The chances that Joe will earn a profit this year are therefore 0.8849 (out of 1). In other words, the chances that Joe will earn a profit are 88.49%.