The Transition From Any Normal Curve to the Standard Curve

In reality, we have an infinite number of possible bell-shaped curves, and not only the standard bell-shaped curve. Each probability distribution has its own expectation and standard deviation, and therefore its own bell-shaped curve. Our ability to calculate probabilities for standard normal distributions is of no use to us (for now) in calculating probabilities for other bell-shaped curves, while these account for most of the actual cases. But the mathematicians have come to our aid again. They have found a way to turn any normal probability distribution (the target curve) into the standard normal probability distribution.

This method is called standardization. Standardization is actually a kind of “translation” of the values of any normal probability distribution into values corresponding to the standard bell-shaped curve (= the standardized values), which enables us to use the table. It therefore follows that almost any problem we want to solve will include two separate operations:

• standardization
• Searching in the table.

The standardized values are called standard units. The standardization operation represents the process of translating the target curve into the standard curve.

Standardization – a Preliminary Pictorial Illustration

Pictorially, the standardization calculation can be compared to a situation where we measure the length of a curved thread.

We will first lay it along a ruler, and then straighten it.

That is what we do with any normal curve (i.e., the target curve). We “lay” it on the standard curve (so that the center of the target curve falls on 0. We then “shape” it exactly in the form of the standard curve, which corresponds to the act of straightening the thread.

Such shaping is possible because the area under both the target curve and the standard curve is equal to 1. “Laying” and “shaping” the target curve is performed through two simple arithmetic operations, subtraction and division, which are performed simultaneously.

“Laying” is performed by subtracting the expectation from every value of the target curve (the number on the X axis). The expectation thereby becomes 0.”Shaping” is performed by dividing the results of this subtraction by the standard deviation of the target curve.

At the end of the process, every value in the target curve (which we will call the original value) has been assigned a corresponding value, which is called the standardized value.

We use the standardized values to calculate the probabilities for the original values in the target curve.

 

 

A Few Examples:

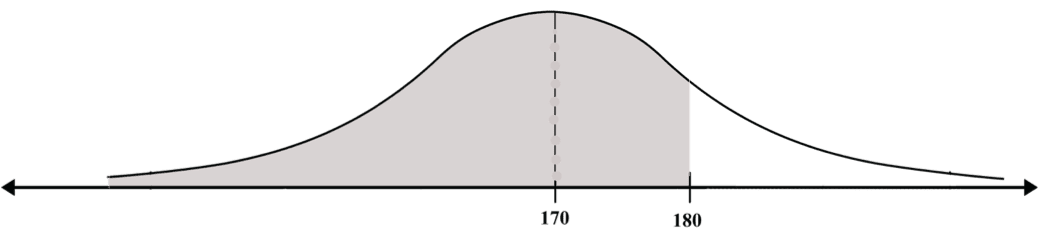
The normal curve in Diagram A represents the probability distribution of the height of 12th grade children. The expectation is μ = 170 centimeters and the standard deviation is σ = 10 centimeters. This normal curve is obviously not a standard curve (in which the expectation is 0 and the standard deviation is 1).

Let’s assume that we wish to calculate the probability that the height of a randomly chosen child will be below 180 centimeters, or, in other words, what proportion of the 12^th grade pupils are shorter than 180 centimeters.

Diagram A:

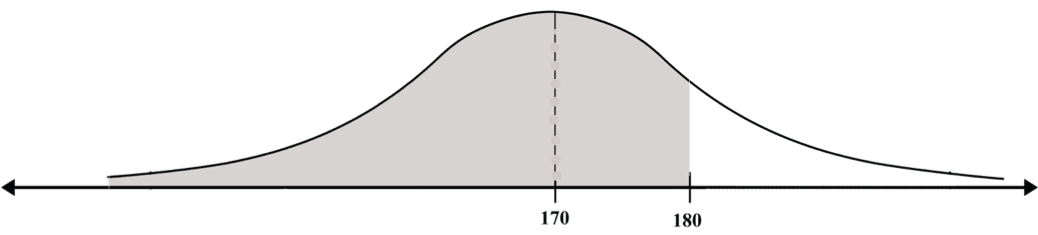
In order to find the standard unit, (the standardized value) of 180, we will subtract the expectation of the probability distribution (170) from 180, and divide the result by the standard deviation of the probability distribution, which gives us:

(180-170)/10 = 10/10 = 1

This means that the standard unit of 180 is 1.

In other words, the value 180 in the target curve is equivalent to the value 1 in the standard curve.

We insert the standard unit (1) in the diagram below the original value (180).

Diagram

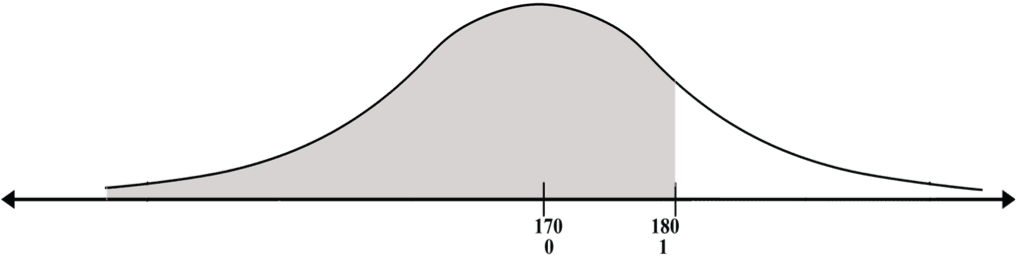
Note: The standard unit of the expectation is always 0. This can be verified by standardizing the expectation: ^(170-170)/₁₀ = ⁰/₁₀ = 0

Instead of asking what percentage of people are below 180, we can now ask what percentage of the area under the standard bell-shaped curve is to the left of 1. What we have actually done is to translate the question from one that we do not know how to answer to an equivalent question that we are able to answer. We use the table to answer the second question, and we see that the area marked in the diagram is 0.8413, i.e., 84.13% of people are shorter than 180 centimeters.

In effect, the operation for “translating” the target curve includes two steps:

1. “Stretching” or “shrinking” the target curve (i.e., the areas that we wish to measure) into the form of the standard normal curve (without changing the numbers on the axis since

the change is only in the gaps between the numbers). This “stretching” or “shrinking” results from the division in the standardization formula.

2. We can move the curve to make it exactly fit the standard normal curve. This moving is accomplished by the subtraction in the standardization formula.