The term “compound interest” denotes the fact that we do not actually pay the interest at the end of the year (or at a different set time as regards the interest payment). The interest is added to the principal, and from that point in time, the interest is calculated on the updated principal.

This can also be described as follows: At the end of the year, we return the principal, as well as the interest, and immediately receive another loan equal to the amount that we have paid off (including principal + interest). Whenever compound interest is involved, we always specify a specific rate of nominal interest, and together these are used as a basis for calculating the compound interest.

Take a short break and watch the following short video which discusses compound interest.

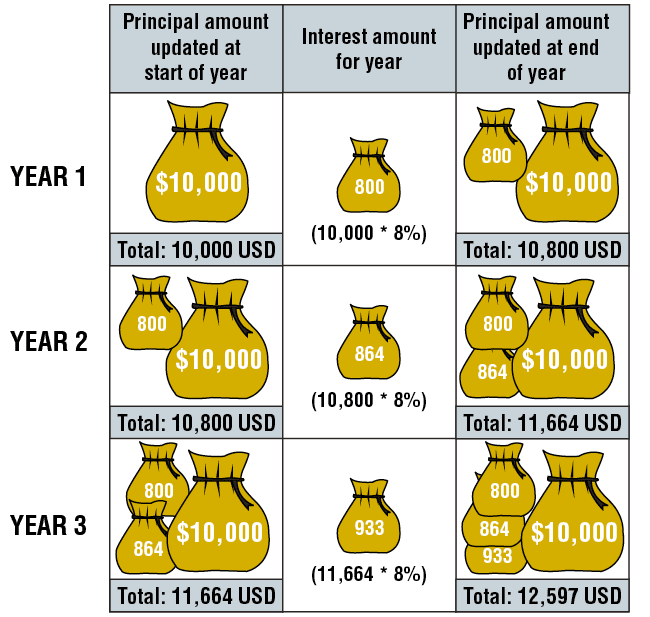
Example: Bill received a $10,000 three-year loan at 8% nominal interest. Both the principal and interest will be paid at the end of the period. What sum of money will Bill repay at the end of three years?

The solution is $12,597.

Compound Interest Formula

Compound Interest= P( 1 + r / n)^ n*t

p = principal amount

r  = annual interest rate (in decimal form)

t  = time the amount is deposited or borrowed E.g 2 years = 2

n  =  how many times the interest is compounded per year 

The stages of the calculation are shown in the following illustration.